Zuordnungen und Graphen
Anwendungsaufgaben im Koordinatensystem
Anwendungsaufgaben kannst du gut im Koordinatensystem darstellen. Ein Punkt im Koordinatensystem hat immer zwei Daten. Die liest du mithilfe der Achsenbeschriftungen ab.

Beispiel:
Achsen: Zuordnung Zeit t in s → Weg s in m
Punkt P(20|400) : Nach 20 s wurden 400 m zurückgelegt.
Das kannst du noch aus dem Graphen ablesen:
- Anwendung: Ein Auto legt in einer bestimmten Zeit einen bestimmten Weg zurück.
- Nach 20 s ist das Auto 400 m vom Startpunkt entfernt.
- Das Auto bleibt 10 s lang stehen.
- Dann entfernt sich das Auto innerhalb von 10 s weitere 400 m vom Startpunkt.
- Das Auto bleibt wieder 10 s lang stehen.
- Das Auto kehrt innerhalb von 10 s die 800 m zurück zum Startpunkt.
Mathematiker sagen, dass der Graph „steigt“ oder „fällt“ oder ein „Plateau“ hat.
Um den Punkt (20|400) in das Koordinatensystem einzuzeichnen, gehst du vom Ursprung des Koordinatensystems (0|0) 20 Einheiten nach rechts und 400 Einheiten nach oben.
Fahrplan der Straßenbahn
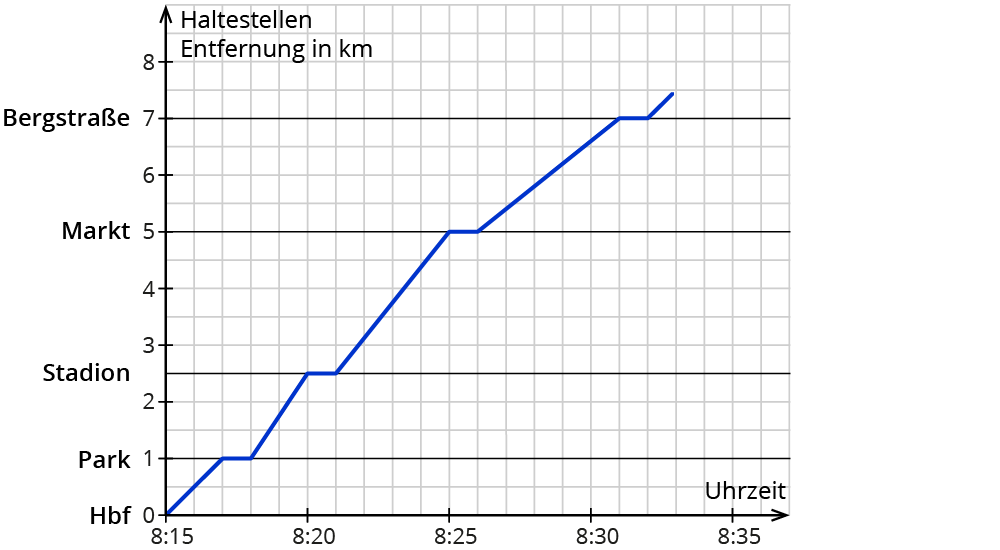
Du siehst in der Abbildung den Fahrplan einer Straßenbahn. Der Straßenbahn sind Zeiten, Haltestellen und Entfernungen zugeordnet.
Zuordnung: Uhrzeit → Haltestelle
Du kannst den Fahrplan als Tabelle schreiben:
| Haltestelle | an | ab |
|---|---|---|
| HBF | 8:15 | |
| Park | 8:17 | 8:18 |
| Stadion | 8:20 | 8:21 |
| Markt | 8:25 | 8:26 |
| Bergstraße | 8:31 | 8:32 |
(HBF = Hauptbahnhof)
Außerdem kannst du ablesen:
- Die Aufenthaltszeit an den Haltestellen beträgt 1 Minute.
- Zwischen den Stationen Park und Stadion fährt die Bahn am schnellsten.
- Zwischen den Stationen Stadion und Markt ist die Entfernung am größten.
- Die längste Fahrzeit beträgt 5 Minuten zwischen den Haltestellen Markt und Bergstr.
Auf dem Schulweg
Schulwege kannst du auch im Koordinatensystem darstellen. Aus den Graphen kannst du Geschichten ablesen oder Aussagen überprüfen.
Du siehst in der Abbildung einige Schulwege.
Ada, Ida, Tim und Tom starten alle von ihrem Zuhause zur Schule.
Diese Aussagen kannst du aus dem Graphen ablesen:
- Tim startet um 7:30 Uhr und kehrt nach 4 Minuten nach Hause zurück.
- Tom läuft am schnellsten los.
- Ada und Ida laufen gleichmäßig schnell zur Schule.
- Ida läuft schneller als Ada und überholt sie um 7:40 Uhr.
- Ab 7:40 Uhr laufen Tom und Ada gleich schnell.
- Tom bleibt 6 Minuten stehen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Füllaufgaben: Form und Graph zuordnen
Unterschiedlich geformte Gefäße werden gleichmäßig mit Wasser gefüllt.
Die Zuordnung Zeit → Füllhöhe kannst du in einem Fülldiagramm darstellen.
Das sind Aufgaben dazu:
- Ordne einem Gefäß den Graphen zu.
- Ordne einem Graphen das Gefäß zu.
Beispiele:

Behälter 1 wird langsamer gefüllt als Behälter 2, da 1 einen größeren Durchmesser hat. Beide Behälter werden aber gleichmäßig gefüllt.

Behälter 3 wird zunächst langsam gefüllt und dann schneller, da sich der Durchmesser plötzlich verkleinert. Du erkennst das an dem Knick des Graphen.
Behälter 4 wird erst schnell und dann immer langsamer gefüllt. Du erkennst das an dem flacher werdenden Verlauf des Graphen.
Anwendungsaufgabe mit Zuordnungstermen
Ein Transportunternehmen benutzt quaderförmige Behälter mit quadratischer Querschnittsfläche und einer Länge von 4 m. Je größer die Seitenlänge x des Quadrates ist, desto größer ist das Behältervolumen.
Zuordnung:
Seitenlänge x in m → Volumen V in m³
Rechenvorschrift:
x → 4 ⋅ x².
Die Zuordnung hat diesen Graphen:

Aus dem Graphen oder der Rechenvorschrift kannst du eine Tabelle erstellen.
| Seitenlänge in m | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Volumen in m³ | 4 | 16 | 36 | 64 |
Mit der Rechenvorschrift oder dem Graphen kannst du diese Frage beantworten: Welches Volumen ergibt sich für eine Seitenlänge von 1,5 m?
Rechenvorschrift: 4 ⋅ x²
Also: 4 ⋅ 1,5²=0
Antwort: 9m³

Das Behältervolumen ergibt sich:
V =4 ⋅ x ⋅ xm³=4 ⋅ x²m³.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen