Bernoulli-Experimente und Bernoulli-Ketten

Du erinnerst dich bestimmt noch daran: Ein Zufallsexperiment bezeichnen wir als Bernoulli-Experiment, wenn es nur genau zwei mögliche Ergebnisse besitzt. Der Zufallsgröße $$X$$, auch Zufallsvariable genannt, werden oft die Werte $$1$$ oder $$0$$ zugeordnet. Dabei bezeichnet die $$1$$ einen Erfolg oder einen Treffer, die $$0$$ einen Misserfolg oder auch eine Niete.
Die Erfolgswahrscheinlichkeit wird mit $$p$$ bezeichnet, die Misserfolgswahrscheinlichkeit dann mit $$q = 1 - p$$.

Eine n-malige Wiederholung ein und desselben Bernoulli-Experiments, bei denen sich die Erfolgswahrscheinlichkeit $$p$$ nicht ändert, bezeichnen wir als n-stufige Bernoulli-Kette oder
n-stufiges Bernoulli-Experiment.

Anzahl von Erfolgen in einer Bernoulli-Kette

Wie kannst Du jetzt die Wahrscheinlichkeit für $$k$$ Erfolge in einer Bernoulli-Kette ermitteln? Angenommen, die Wahrscheinlichkeit für einen Erfolg sei $$p$$, dann hat jedes Ergebnis mit genau $$k$$ Erfolgen die Wahrscheinlichkeit $$p^k * (1 - p)^(n-k)$$.

Wie viele Möglichkeiten es gibt nun, aus $$n$$ Vorgängen die $$k$$ Teilvorgänge auszuwählen? Diese Überlegung führt auf den sog. Binomialkoeffizienten, der die gesuchte Anzahl als Kombination ohne Wiederholung und ohne Beachtung der Reihenfolge beschreibt. Schau Dir die Idee anhand dieses Beispiels an:

Du hast 4 Objekte A, B, C, D, aus denen Du 2 Objekte in einer Bernoulli-Kette auswählen sollst. Du kommst auf die möglichen Kombinationen:
AB, AC, AD, BC, BD, CD,
also 6 Möglichkeiten.

Dafür gibt es auch eine Formel, nämlich den sog. Binomialkoeffizienten
$$((n),(k))=(n!)/(k!*(n-k)!)$$.

In unserem Beispiel ist $$n = 4$$ und $$k =2$$ und somit $$((4),(2))= (4*3)/(1*2)=6$$.

Der Binomialkoeffizient liefert dir die Anzahl der Erfolge - jetzt musst du dies noch mit der Erfolgswahrscheinlichkeit kombinieren und kommst auf folgende Aussage:

In einer Bernoulli-Kette der Länge $$n$$ mit Erfolgswahrscheinlichkeit $$p$$ treten genau $$k$$ Erfolge mit folgender Wahrscheinlichkeit auf:

$$P(k)=((n),(k)) * p^k * (1-p)^(n-k)$$.

Formel von Bernoulli

Die Anzahl der Erfolge in einer Bernoulli-Kette werden, genauso wie in einem Bernoulli-Experiment, als Zufallsgröße bzw. Zufallsvariable $$X$$ bezeichnet. $$X$$ kann jetzt jedoch nicht nur die Werte $$0$$ oder $$1$$, sondern die ganzzahligen Werte von $$0$$ bis $$n$$ annehmen.

Man nennt diese Formel Bernoulli-Formel und schreibt für die Wahrscheinlichkeit, dass bei Erfolgswahrscheinlichkeit $$p$$ genau $$k$$ Erfolge erzielt werden,

$$P(X=k) = B(n; p; k) = ((n),(k)) * p^k * (1-p)^(n-k) $$.

Beispiel Urnenexperiment:
Eine Urne enthält 6 rote und 8 grüne Kugeln. Es werden 5 Kugeln mit Zurücklegen entnommen. Wie hoch ist die Wahrscheinlichkeit, dass dabei genau 4 rote Kugeln entnommen wurden?
Hier ist die Kettenlänge $$n = 5$$,
der Erfolg „Rote Kugel ziehen“ mit der
Erfolgswahrscheinlichkeit $$p = 6/14 = 3/7 $$ .
Mit der Bernoulli-Formel erhalten wir

$$P(X=4) = B(5; 3/7; 4) = ((5),(4)) * (3/7)^4 * (4/7)^(1) approx 0,0964$$

Mehrere Erfolgsmöglichkeiten

Oft werden Aufgaben gestellt, bei denen es nicht um „genau“ $$X=k$$ Treffer geht, sondern um z.B. „höchstens $$X=k=5$$“ oder „mindestens $$X=k=3$$“ Treffer erzielt werden sollen.
Du kannst dann einfach die passenden Trefferwahrscheinlichkeiten addieren oder subtrahieren.

Beispiel:
Bei einem Bernoulli-Experiment sei $$p=0,7$$ und $$n=6$$. Berechne die Wahrscheinlichkeit dafür, dass höchstens $$2$$ Treffer erzielt werden.
Lösung: $$P(X=k<=2)=P(X=k=0)+P(X=k=1)+P(X=k=2)=$$
$$=((6),(0))*0,7^0*0,3^6 + ((6),(1))*0,7^1*0,3^5+((6),(2))*0,7^2*0,3^4 approx 0,7443$$
Die Wahrscheinlichkeit, dass in diesem Fall höchstens $$2$$ Treffer erzielt werden, beträgt ca. $$0,7443$$.

Binomialverteilung

Betrachtest Du für gegebenes $$n$$ und $$p$$ nun alle möglichen Wahrscheinlichkeiten für die $$k$$ möglichen Erfolge, kommst Du auch die sogenannte Binomialverteilung .

Nimm dazu als Beispiel eine Bernoulli-Kette mit der Länge $$n=5$$ und der Trefferwahrscheinlichkeit $$p = 0,4$$.

Berechnest Du alle möglichen Erfolgswahrscheinlichkeiten für die $$k$$ möglichen Treffer zwischen $$0$$ und $$5$$ erhältst Du eine Tabelle mit diesen Werten:

Die Tabelle liefert die sogenannte Wahrscheinlichkeitsverteilung einer Bernoulli-Kette, die Binomialverteilung . Oft wird die graphische Darstellung einer Binomialverteilung in Form eines Histogramms modelliert:

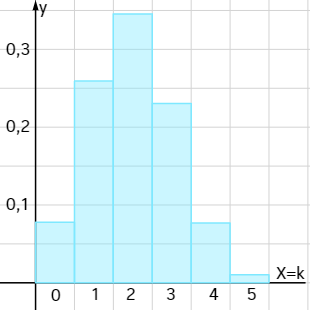
Die Werte für die Binomialverteilung kannst Du aus Tabellen ablesen oder mit Taschenrechnern berechnen.