SuS können Erwartungswert und Standardabweichung in Anwendungsaufgaben bestimmen
Erwartungswert
Zufallsexperimente liefern Häufigkeits- bzw. Wahrscheinlichkeitsverteilungen ihrer Zufallsgröße X. Aber wie kannst Du herausfinden, welchen Wert der Zufallsvariablen Du auf lange Sicht erwarten kannst?
Schaue dir dieses Beispiel an:
Bei einem Glücksspiel mit X als Gewinn sei die Wahrscheinlichkeitsverteilung von X:
| x in Euro | 0 | 0,50 | 1,00 | 2,00 | 5,00 |
| P(X=x) | 0,70 | 0,10 | 0,10 | 0,08 | 0,02 |
Wie kannst Du vorgehen, um Deinen voraussichtlichen Gewinn zu berechnen? Eine naheliegende Idee ist es, die Gewinnhöhe immer mit ihrer Wahrscheinlichkeit zu multiplizieren und alles zu addieren - denn da die Wahrscheinlichkeiten sich immer zu 1 addieren, hast Du gleich eine Art Durchschnitt mitberechnet.
In diesem Beispiel wäre dies
0⋅0,70+0,50⋅0,10+1,00⋅0,10+2,00⋅0,08+5,00⋅0,02=0,41
Anschaulich heißt das: Wenn du dieses Spiel sehr oft spielen würdest, würde dein durchschnittlicher Gewinn etwa 0,41€ betragen. Bei einem Einsatz von 1€ würdest du im Durchschnitt also pro Spiel 0,59€ verlieren.
Dieses Beispiel motiviert zu folgender Defintion:
Nimmt eine Zufallsgröße X die Werte x1,x2,…,xn an, so nennen wir
E(X)=x1⋅P(X=x1)+… …+xn⋅P(X=xn) Erwartungswert der Zufallsgröße X.
Wir notieren statt E(X) oft auch kurz µ.
Der Erwartungswert ist im obigen Beispiel also E(X)=0,41€. Er wird oft auch als „Mittelwert“ einer Wahrscheinlichkeitsverteilung betrachtet.
Für X als binomialverteilter Zufallsgröße mit den Parametern n als Anzahl
der Versuche und p als Trefferwahrscheinlichkeit gilt für den Erwartungswert µ
µ=n⋅p.
Standardabweichung
Mit dem Erwartungswert alleine lässt sich die Wahrscheinlichkeitsverteilung einer Zufallsgröße jedoch oft nur ungenau beschreiben. Schau dir dazu diese Abbildungen von Wahrscheinlichkeitsverteilungen an:
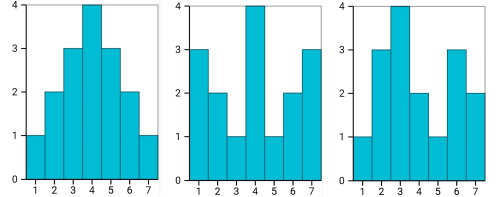
Alle drei Verteilungen haben den Erwartungswert 4. Die Streuung der Wahrscheinlichkeitsverteilung ist recht unterschiedlich und zeigt nicht, wie sich die einzelnen P(X)-Werte zum Erwartungswert gruppieren - ob sie sich z.B. um den Erwartungswert symmetrisch gruppieren oder wie im letzten Bild unsymmetrisch angeordnet sind.
Die Streuung der Werte von X um E(X) wird u.a. durch die Standardabweichung σ(X) erfasst.
Wir hatten für den Erwartungswert festgelegt - hier mit einer geeigneten Erweiterung:
E(X)=x1⋅P(X=x1)+x2⋅P(X=x2)+…+xn⋅P(X=xn)=n∑i=1xi⋅P(X=xi)
Wir bezeichnen die Streuung einer Wahrscheinlichkeitsverteilung als Standardabweichung σ(X)
σ(X)=√n∑i=1(xi-E(X))2⋅P(X=xi)
Für die Berechnung der Standardabweichung bei einer Binomialverteilung mit n als Anzahl der Versuche, p als Trefferwahrscheinlichkeit und q=(1-p) als Wahrscheinlichkeit für eine Niete gilt folgende Formel
σ=√n⋅p⋅(1-p)=√n⋅p⋅q.
Standardabweichung im Beispiel
Wir wollen die Standardabweichung für das Beispiel des Glücksspiels berechnen, für das wir den Erwartungswert von 0,41 ermittelt hatten. Wir lassen zur einfacheren Darstellung das €-Zeichen weg.
Wir notieren noch einmal die Wahrscheinlichkeitsverteilung:
| xi | 0 | 0,50 | 1,00 | 2,00 | 5,00 |
| P(X=xi) | 0,70 | 0,10 | 0,10 | 0,08 | 0,02 |
Wir hatten den Erwartungswert E(X)=0,41 berechnet.
Nun berechnen wir die Standardabweichung:
σ(X)=√(0-0,41)2⋅0,7+(0,50-0,41)2⋅0,1+(1-0,41)2⋅0,1+(2-0,41)2⋅0,08+(5-0,41)2⋅0,02
σ(X)=√3,7769≈1,94
Erwartungswert und Standardabweichung
Wir schauen uns mal die Werte der unsymmetrischen Beispiel-Verteilung an:
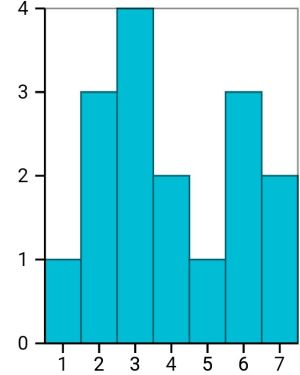
Wahrscheinlichkeitsverteilung in Tabellenform:
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X=xi) | 0,0625 | 0,1875 | 0,25 | 0,125 | 0,0625 | 0,1875 | 0,125 |
Erwartungswert:
E(X)=1⋅0,0625+2⋅0,1875+3⋅0,25+4⋅0,125+5⋅0,0625+6⋅0,1875+7⋅0,125=4
Standardabweichung:
σ(X)=√(1-4)2⋅0,0625+(2-4)2⋅0,1875+(3-4)2⋅0,25 +(4-4)2⋅0,125+(5-4)2⋅0,0625+(6-4)2⋅0,1875+(7-4)2⋅0,0625
σ(X)=√3,5≈1,87
Vergleich dazu ist die Standardabweichungs der Verteilung
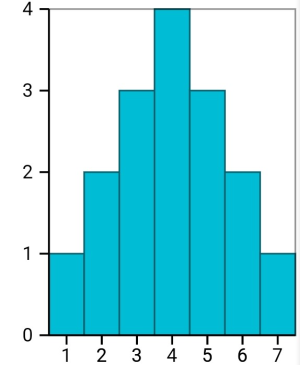
σ(X)=√2,5≈1,57
Die größere Streuung der Werte der Zufallsgröße macht sich in einer größeren Standardabweichung bemerkbar. So können Wahrscheinlichkeitsverteilungen noch genauer beschrieben werden.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen


