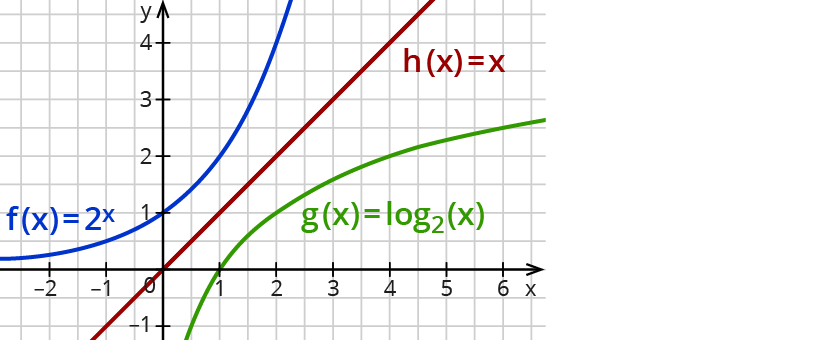
Den Logarithmus untersuchen
Blick zurück: Potenzieren und Wurzelziehen
Das Berechnen einer Potenz der Art bx nennt man Potenzieren.
Beispiel: 24=2⋅2⋅2⋅2=16
Was ist aber, wenn du die Basis suchst? Das Potenzieren kannst du umkehren.
Beispiel: 4√16=2, denn 2⋅2⋅2⋅2=16
Das Wurzelziehen ist die Umkehrung des Potenzierens.
Was ist der Logarithmus?
Was ist, wenn du den Exponenten suchst?
Beispiel:
2x=16
Womit musst du 2 potenzieren, um auf 16 zu kommen? Das Ergebnis weißt du schon: es ist 4.
Genau das macht der Logarithmus.
Der Logarithmus von 16 zur Basis 2 ist die Zahl, mit der du 2 potenzierst, um 16 rauszukriegen.
Schreibe: log216=4, denn 24=2⋅2⋅2⋅2=16.
Lies: Der Logarithmus von 16 zur Basis 2 ist gleich 4.
Mit dem Logarithmus bestimmst du den Exponenten.
Definition von Logarithmen
Es seien y und b≠1 zwei positive Zahlen. Dann ist der Logarithmus von y zur Basis b diejenige Zahl x, mit der man b potenzieren muss, um y zu erhalten.
Um die Gleichung 2x=16 zu lösen, schreibst du log216.
Die Ausdrücke 2x=16 und log216 sind also gleichbedeutend.
Also:
log216=4, da 24=2⋅2⋅2⋅2=16.
Taschenrechner können log216 berechnen. Probiere es aus. Er wird 4 anzeigen.
bx=y bedeutet dasselbe wie logby=x .


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispiele (1)
Diese Beispiele kannst du alle ohne Taschenrechner nur durch Überlegen lösen:
log1010000=4 , da 104=10⋅10⋅10⋅10=10000
log10101000=-3, da 10-3=1103=11000
log381=4 , da 34=3⋅3⋅3⋅3=81
log142=-12,
da (14)-12=(14-1)12=412=√4=2
bx=y bedeutet dasselbe wie logby=x .
Beispiele (2)
Folgende Beispiele kannst du alle ohne Taschenrechner nur durch Überlegen lösen:
log5525=-2 ,
da 5x=125 ⇔ 5x=152 ⇔ 5x=5-2 ⇔ x=-2
log5125=3,
denn b3=125 ⇔ b3=53 ⇔ b=5
log3343=7,
denn 73=y ⇔ y=343
log91=0,
denn 90=y ⇔ y=1
log3√3=0,5,
da 3x=√3 ⇔ 3x=30,5 ⇔ x=0,5
bx=y bedeutet dasselbe wie logby=x .
Potenzgesetze:
1an=a-n
√a=a12=a0,5
Was es sonst noch zu wissen gibt
a) Logarithmen von negativen Zahlen existieren nicht, da bx stets positiv ist, wenn b>0 ist .y kann daher nicht den Wert 0 annehmen.
b) Da der Logarithmus zur Basis 10 häufig gebraucht wird, schreibt man als Konvention auch log10(y)=log(y).
Die 10 darfst du als Basis also weglassen.
c) b1=b, also logbb=1 für alle b>0.
d) b0=1, also logb1=0 für alle b>0.
d) Der Fall b=1 wird ausgeschlossen, da 1x stets gleich 1 ist für alle x>0.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen