Logarithmus und Potenzieren

Zur Erinnerung: Der Logarithmus von $$y$$ zur Basis $$b$$ ist diejenige Zahl $$x$$, mit der man $$b$$ potenzieren muss, um $$y$$ zu erhalten.

Beispiele:
a) $$log_2 (8)=3$$, da $$2^3=8$$.

b) $$log_2 (32)=4$$, da $$2^4=3$$

c) $$log_9 (1/81)=log_9 (1/(9^2))$$$$=log_9 (9^-2)=-2$$,
   da $$9^-2=1/81$$

Das Hoch-$$x$$-rechnen machst du mit dem Logarithmus rückgängig.

Hoch-$$x$$-rechnen und den Logarithmus bilden sind also Umkehroperationen.

$$log_b (b^x)=x$$ und $$b^(log_b x)=x$$.

Logarithmengesetze:

Für Logarithmen zur Basis $$b$$ mit $$b≠1$$ und $$b>0$$ und für positive reelle Zahlen $$u$$ und $$v$$ sowie eine reelle Zahl $$r$$ gilt:

$$log_b (u*v) = log_b (u) + log_b (v)$$

$$log_b(u/v)=log_b(u)-log_b(v)$$

$$log_b(u^r)=r*log_b (u)$$

Logarithmusfunktion der Exponentialfunktion

Dieses Umkehrprinzip kannst du auf Funktionen übertragen.

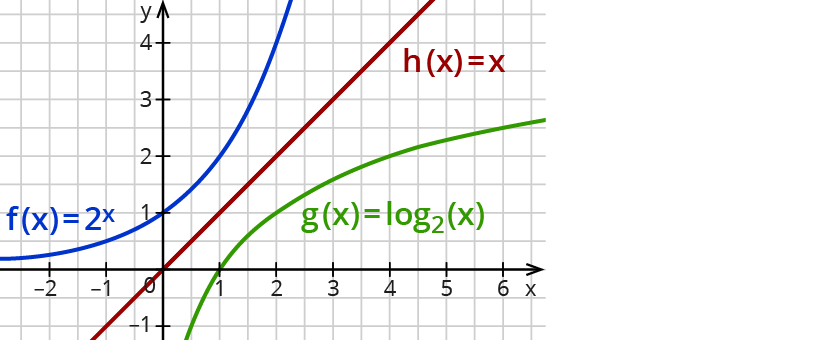
Die Exponentialfunktion $$y=b^x$$ $$(b≠0)$$ und die Logarithmusfunktion $$y=log_b(x)$$ (mit $$x>0$$, $$b>0$$, $$b≠1$$) sind Umkehrfunktionen.

Graphisch entsteht die Logarithmusfunktion durch Spiegelung der Exponentialfunktion an der Ursprungsgerade $$y=x$$.

Beispiel:
$$f(x)=2^x$$ und $$g(x)=log_2 (x)$$.

Eine Funktion mit der Gleichung $$y=log_b (x)$$ mit $$x>0$$ heißt Logarithmusfunktion zur Basis $$b$$, wobei $$b>0$$ und $$b≠1$$.

Eigenschaften der Logarithmusfunktionen

Hier siehst du die Graphen von Logarithmusfunktionen mit verschiedenen Basen $$b$$:

• Der Graph der Funktion $$y=log_b(x)$$ steigt für $$b>1$$ und fällt für $$0<b<1$$.
• Der Graph der Funktion $$y=log_b(x)$$ liegt rechts von der $$y$$-Achse. Für nicht-positive $$x$$-Werte ist die Funktion nicht definiert.
• Alle Graphen verlaufen durch den Punkt $$P(1|0)$$. Das ist gleichzeitig die Nullstelle aller Graphen. $$P(1|0)$$ ist der einzige Punkt, in dem sich die Graphen treffen.
• Jede Logarithmusfunktion der Form $$y=log_b (x)$$ verläuft durch den Punkt $$(b|1)$$.
• Der Graph schmiegt sich für $$b>1$$ dem negativen und für $$0<b<1$$ dem positiven Teil der $$y$$-Achse an.
• Für $$b>1$$: Für $$x>1$$ verläuft der Graph oberhalb der $$x$$-Achse, für $$0<x<1$$ unterhalb der $$x$$-Achse.
• Für $$0<b<1$$ ist es genau umgekehrt.
• Je dichter $$b$$ bei $$1$$ ist, desto stärker wird der Graph eine Parallele zur $$y$$-Achse und wäre dann keine Funktion mehr.

Funktionsgleichung aus einem Punkt bestimmen

Du hast gesehen, dass die Graphen der Logarithmusfunktionen $$y=log_b (x)$$ nur genau einen Punkt gemeinsam haben. Jeder andere Punkt legt deshalb eindeutig eine Logarithmusfunktion fest. Wenn du einen Punkt hast, kannst du die Funktion bestimmen!

Beispiele:
Bestimme diejenige Logarithmusfunktion, die durch den Punkt $$(2|2)$$ verläuft. Du setzt dazu die Koordinaten von $$P$$ ein und stellst nach $$b$$ um:

   $$y=log_b (x)$$

$$⇔2=log_b (2)$$

$$⇔b^2=2$$  $$| sqrt$$

$$⇔b=+-sqrt(2)$$

$$-sqrt(2)$$ ist als Lösung auszuschließen. Deshalb ist die gesuchte Funktionsgleichung $$y=log_(sqrt(2)) (x)$$.