Exponentialfunktionen der Form $$y=b^x$$

Bei Exponentialfunktionen ist das Neue, dass die Veränderliche (das $$x$$) im Exponenten steht, also die Hochzahl ist.

Beispiel: $$y=2^x$$.

Ist $$x$$ beispielsweise $$4$$, ist der Funktionswert $$ =2^4= 2*2*2*2=16$$.

Diese Funktionen können genauso wie andere mithilfe von Graphen oder Wertetabellen dargestellt werden.

Die Wertetabelle von $$y=2^x$$

Du siehst nun für diese Funktion eine Wertetabelle:

Der Funktionswert $$y$$ verdoppelt sich mit jedem Schritt nach rechts in der Tabelle.

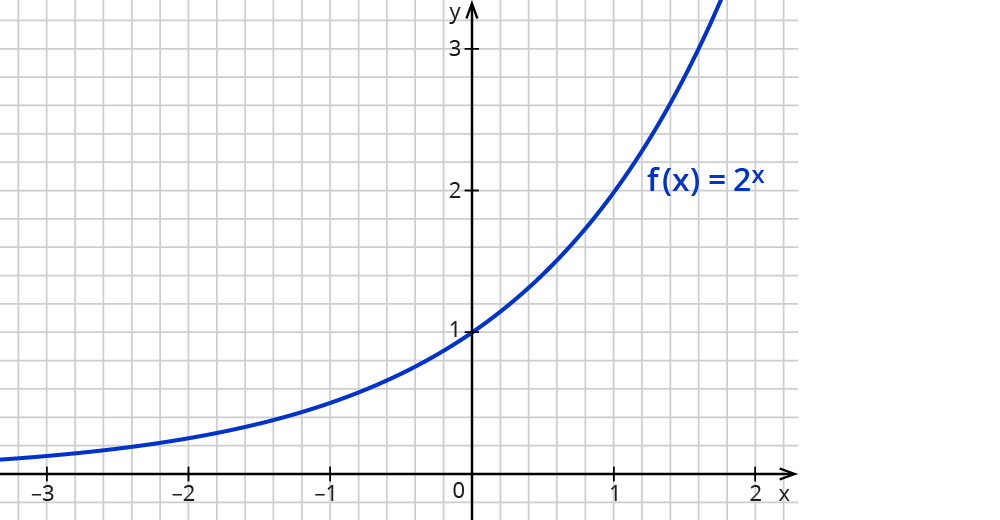
Der Graph von $$y=2^x$$

Trägst du die $$x$$- und $$y$$-Werte ins Koordinatensystem ein, erhältst du folgenden Graphen:

Wie du sehen kannst, steigt der Graph. Die Funktion beschreibt also exponentielles Wachstum. Würde der Graph fallen, hättest du es mit exponentiellem Zerfall zu tun.

Definition: Exponentialfunktionen der Form $$y=b^x$$

Eine Funktion mit der Gleichung $$y=b^x$$ mit $$b>0$$ und $$b\ne1$$ heißt Exponentialfunktion zur Basis $$b$$.

Das $$b$$ wird auch Wachstums- bzw. Zerfallsfaktor genannt.

Der Fall $$b=1$$ wird hierbei auch ausgeschlossen, weil für $$b=1$$ dort $$y=1^x$$ steht. Das Ergebnis davon ist stets $$1$$, da hierbei lediglich die Zahl $$1$$ beliebig oft mit sich selbst multipliziert wird.

Und wieso soll $$b$$ nicht negativ sein?

Das ist die Wertetabelle zu $$y=(-2)^x$$:

Du siehst, dass die $$y$$-Werte von $$+$$ nach $$–$$ springen. Stell dir das mal im Koordinatensystem vor:
Die Punkte kannst du nicht mit einer Linie verbinden.

Solche Funktionen kommen im Alltag nicht vor, deshalb musst du sie auch nicht untersuchen.:-)

Eigenschaften von Exponentialfunktionen der Form $$y=b^x$$

Betrachte die Graphen und entdecke allgemeine Eigenschaften.

An den Graphen kannst du sehen:

• Der Graph fällt für $$b$$ zwischen $$0$$ und $$1$$ (exponentieller Zerfall) und steigt für $$b$$ größer $$1$$ (exponentielles Wachstum).

• Die Graphen liegen alle oberhalb der $$x$$-Achse. Es gibt also keine negativen $$y$$-Werte. Die 0 ist auch kein $$y$$-Wert.

• Die Graphen schmiegen sich der $$x$$-Achse an.

• Alle Graphen verlaufen durch den Punkt $$P(0|1)$$.

• Ist die Basis $$b$$ ganz dicht bei $$1$$, ähnelt der Graph einer Geraden mit $$y=1$$.

Bestimmen der Funktionsgleichung bei gegebenem Punkt

Du hast bereits gesehen, dass sich die Graphen aller Exponentialfunktionen der Form $$y=b^x$$ im Punkt $$(0|1)$$ schneiden. Sie haben tatsächlich nur diesen gemeinsam! Die folgende Rechnung macht das plausibel.

Du hast den Punkt $$(7|3)$$ gegeben und sollst die dazugehörige Funktionsgleichung angeben:

$$y=b^x$$     | Punkt einsetzen

$$3=b^7$$     | $$root7$$

$$b=$$ $$root7 3≈ 1,17$$

$$⇒ y ≈ 1,17^x$$

Die zuletzt beschriebene Funktion enthält diesen Punkt, und zwar nur diese! Sobald sich $$x$$ oder $$y$$ ändert, ändert sich auch das $$b$$.