Wachstum rekursiv beschreiben
Rekursive und direkte Berechnung von Guthaben
Um exponentielle Prozesse zu berechnen, gibt es 2 Möglichkeiten:
rekursiv, indem du schrittweise das n-te Glied mit dem Wachstumsfaktor multiplizierst, um auf das nächste zu kommen: an+1=an⋅q.
explizit oder direkt durch eine Formel: an=…
Rekursiv (lat.): zurückgehend auf Bekanntes
Rekursive Berechnung
Frau Müller möchte Geld sparen. Dazu zahlt sie 3000 € auf ein Sparkonto ein. Die Bank verzinst das Guthaben mit 3,5 % jährlich. Die Zinsen werden dem Guthaben zugeschlagen und dann mitverzinst. Wie viel Geld ist nach 5 Jahren auf dem Konto?
Variante A:
Der Zinssatz ist 3,5 %, also ist der Zinsfaktor (oder Wachstumsfaktor) 1,035.
| Guthaben nach 0 Jahren a0: | 12000 € |
| Guthaben nach 1 Jahr a1: | 12000 €⋅1,035=12420 € |
| Guthaben nach 2 Jahren a2: | 12420 €⋅1,035=12854,70 € |
| Guthaben nach 3 Jahren a3: | 12854,70 €⋅1,035=13304,61 € |
| Guthaben nach 4 Jahren a4: | 13304,61 €⋅1,035=13770,28 € |
| Guthaben nach 5 Jahren a5: | 13770,28 €⋅1,035=14252,24 € |
Willst du jetzt z. B. a6 wissen, musst du a5 nehmen und wieder mit 1,035 multiplizieren.
a6=a5⋅1,035=14252,24 €⋅1,035=…
Oder allgemein: an+1=an⋅q
Der Nachteil hieran ist, dass man schrittweise vorgehen muss. Um den (n+1)-ten Wert zu berechnen, muss der n-te Wert bekannt sein.
Den Zinsfaktor q für den Zinssatz p berechnest du mit q=1+p100.
Direkte Berechnung
Frau Müller möchte Geld sparen. Dazu zahlt sie 3000 € auf ein Sparkonto ein. Die Bank verzinst das Guthaben mit 3,5 % jährlich. Die Zinsen werden dem Guthaben zugeschlagen und dann mitverzinst. Wie viel Geld ist nach 5 Jahren auf dem Konto?
Variante B:
Der Zinssatz ist 3,5 %, also ist der Wachstumsfaktor 1,035.
| Guthaben nach 1 Jahr a1: | 12000 €⋅1,0351=12420 € |
| Guthaben nach 2 Jahren a2: | 12000 €⋅1,0352=12854,70 € |
| Guthaben nach 3 Jahren a3: | 12000 €⋅1,0353=13304,61 € |
| Guthaben nach 4 Jahren a4: | 12000 €⋅1,0354=13770,28 € |
| Guthaben nach 5 Jahren a5: | 12000 €⋅1,0355=14252,24 € |
Guthaben nach n Jahren an: an=12000⋅1,035n
In diese Formel muss nur noch das n eingesetzt werden und du bekommst die entsprechende Lösung. So ist es im Gegensatz zu Variante A kein Problem, das Guthaben für ein beliebiges Jahr auszurechnen.
Den Zinsfaktor q für den Zinssatz p berechnest du mit q=1+p100.
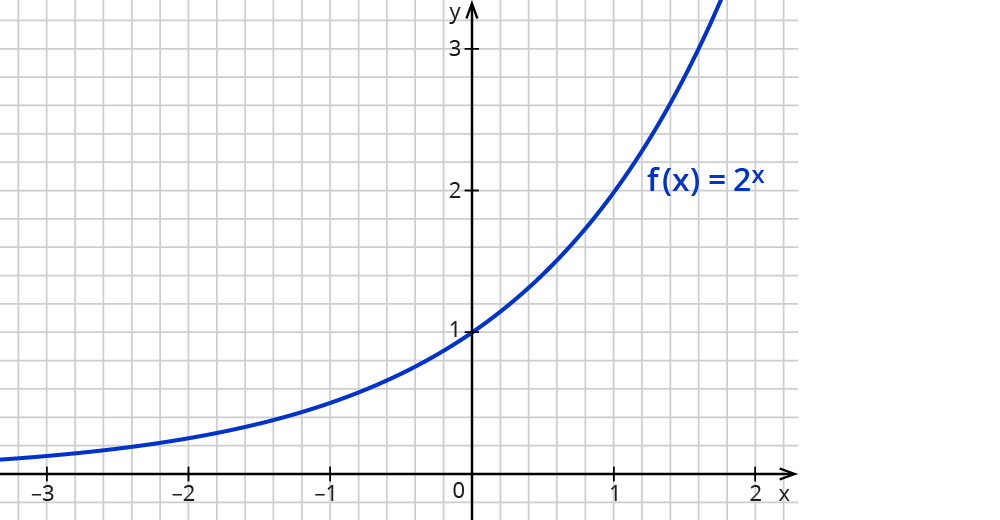
Die direkte Berechnung kennst du schon als exponentielles Wachstum mit der allgemeinen Form f(x)=a⋅bx mit b>0 und b≠1

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Zahlenfolgen
Bei den Zinseszinsen hast du zu jedem Jahr das Guthaben notiert. Allgemein: Jeder natürlichen Zahl (0,1, 2, 3, …) hast du eine reelle Zahl an zugeordnet. Mathematiker nennen so eine Zuordnung Zahlenfolge.
Die Zahlen an heißen Folgenglieder.
Zahlenfolgen kannst du rekursiv und explizit angeben.
Beispiel:
Folge der geraden Zahlen
| n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| an | a0=0 | a1=2 | a2=4 | a3=6 | a4=8 |
Wie findest du die Vorschriften?
Rekursiv: Von Folgeglied zu Folgeglied addierst du 2. Du nimmst also ein beliebiges Folgeglied an und rechest +2. So erhältst du das nächste Folgeglied an+1. Außerdem gibst du immer das Startglied an: a0 ist 0. Vorschrift: an+1=an+2
a0=0
Explizit: Von n zu an kommst du, indem du mal 2 rechnest.
an=2n
Noch ein Beispiel
Wie im Beispiel oben lässt sich auch die Zahlenfolge der ungeraden Zahlen rekursiv und explizit angeben.
| n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| an | a0=1 | a1=3 | a2=5 | a3=7 | a4=9 |
Rekursiv: Von Folgeglied zu Folgeglied addierst du 2. Das Startglied ist 1.
an+1=an+2 und a0=1.
Explizit: Von n zu an kommst du, indem du mal 2 und plus 1 rechnest.
an=2n+1.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen