Anwendungsaufgaben Wachstum und Abnahme
Immer wieder die gleichen Probleme
Erinnere dich nochmal schnell an das Beispiel mit dem Taschengeld:
Michael und Peter sind Zwillinge und gerade 14 Jahre alt geworden. Es stehen die Verhandlungen für mehr Taschengeld an. Zur Zeit bekommen beide 5 €.
Michael schlägt seinem Vater vor, jeden Monat 1 € mehr zu bekommen. Peter hingegen möchte 10 % pro Monat mehr. Michael sagt: „Da habe ich immer mehr Geld als du, bis meine Ausbildung mit 16 beginnt.“ Peter sagt: „Du täuschst dich!“
Bei solchen Aufgaben kannst eine Menge aus den Graphen der Funktionen ablesen.
Der Schnittpunkt
Schaust du dir die beiden Funktionsgraphen an, siehst du bei S1(0;5) und S2(14;19) einen Schnittpunkt.
Zum Zeitpunkt 0 haben die Brüder das gleiche Taschengeld (5 €) und im 14. Monat haben beide 19 € bekommen.
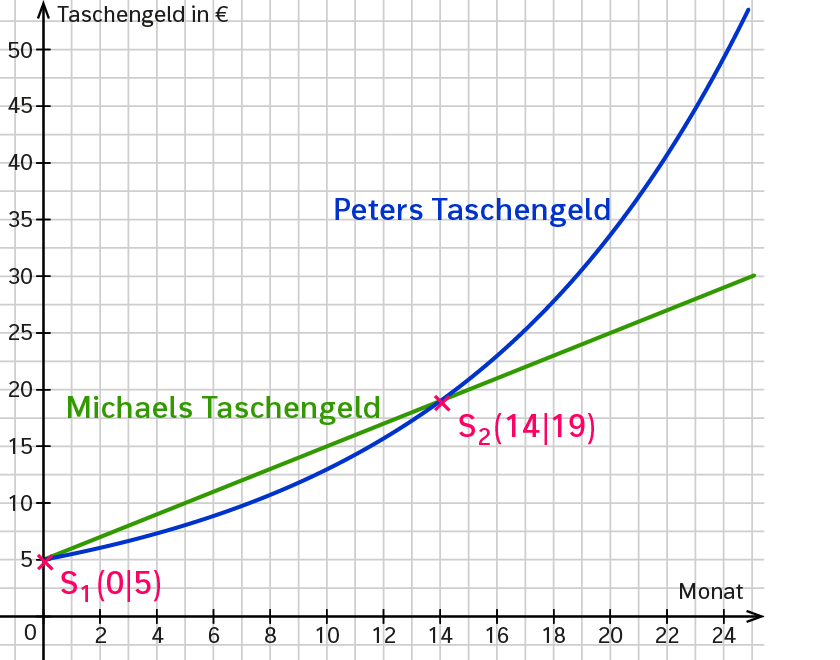
Willst du von zwei verschiedenen Wachstumsarten wissen, wann beide Funktionen denselben Wert haben, bestimmst du den Schnittpunkt. Den kannst du am Funktionsgraphen ablesen oder mit der Wertetabelle bestimmen.

Ist das bezahlte Taschengeld nicht ungerecht?
Peter und Michaels Vater hat sich auch mit dem Problem beschäftigt. Er hat aufgeschrieben, wie viel Taschengeld er insgesamt in den zwei Jahren bezahlen muss.
| Monat | Peters Taschengeld in € | Michaels Taschengeld in € |
|---|---|---|
| Januar | 5 | 5 |
| Februar | 5,50 | 6 |
| März | 6,10 | 7 |
| April | 6,70 | 8 |
| Mai | 7,40 | 9 |
| Juni | 8,10 | 10 |
| Juli | 8,90 | 11 |
| August | 9,80 | 12 |
| September | 10,80 | 13 |
| Oktober | 11,90 | 14 |
| November | 13,10 | 15 |
| Dezember | 14,40 | 16 |
| Januar | 15,80 | 17 |
| Februar | 17,40 | 19 |
| März | 19,10 | 19 |
| April | 21 | 20 |
| Mai | 23,10 | 21 |
| Juni | 25,40 | 22 |
| Juli | 27,90 | 23 |
| August | 30,70 | 24 |
| September | 33,80 | 25 |
| Gesamtsumme | 321,90 | 315 |
Aus der Differenz der beiden Summen erfährt der Vater der Zwilllinge, dass er Michael zu Beginn seiner Ausbildung noch 6,90 € geben muss.
Bei einigen Anwendungen ist die Gesamtsumme wichtig. Addiere dazu alle Beträge auf. Das brauchst du zum Beispiele bei der Kontostandsberechnung.
Pflanzenwuchs

Bild: iStockphoto.com/Sjo
Ein Teich hat eine Oberfläche von 64 m². Der Besitzer hat einige besonders schöne und schnell wachsende Seerosen gepflanzt. Die Pflanzen bedecken schon 1m² der Oberfläche. Schöpft er sie nicht ab, verdoppelt sich die von Pflanzen bedeckte Fläche alle 6 Tage. Der Besitzer schafft es, maximal innerhalb von 6 Tagen 8m² zu reinigen.
a) Bestimme, wann der Teich vollständig bedeckt ist, wenn der Besitzer nicht abschöpft.
b) Nach wieviel Tagen kann der Besitzer selbst durch Abschöpfen den Teich nicht mehr pflanzenfrei bekommen?
Lösung
Mit Funktionsgraph
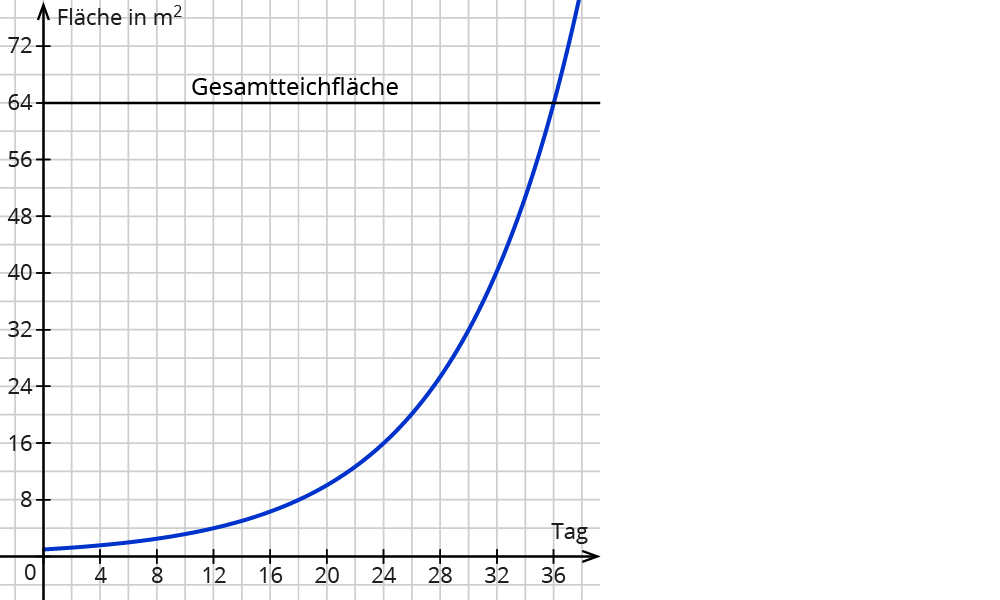
a) Aus dem Funktionsgraphen kannst du ablesen, dass nach 36 Tagen die bewachsene Fläche genauso groß ist wie die Teichfläche. Dies ist wieder der Schnittpunkt.
b) Das kannst du leider nicht direkt ablesen.
Mit einer Wertetabelle
Wenn du keinen Graphen hast oder er dir nicht weiterhilft, erstellst du eine Wertetabelle.
Die Tabelle lässt sich jeweils alle 6 Tage auffüllen. Der erste Tag ist Tag 0. Zu diesem Zeitpunkt sind gerade 1 m² bedeckt.
Alle 6 Tage wird die bewachsene Fläche verdoppelt. Deshalb trägst du am Tag 6 bei der bewachsenen Fläche 2m² ein, denn: 2 ⋅1 m² = 2 m².
Die Zunahme errechnet sich aus der Differenz zur vorangegangenen Fläche. Innerhalb von 6 Tagen verdoppelt sich die Fläche von 1m² auf 2 m². Sie wird also um 2m² -1m² = 1m² größer.
| Tag | bewachsene Fläche in m² | Zunahme zum vorangegangenen Abschnitt in m² |
|---|---|---|
| 0 | 1 | 0 |
| 6 | 2⋅1=2 | 2-1=1 |
| 12 | 2⋅2=4 | 4-2=2 |
| 18 | 2⋅4=8 | 8-4=4 |
| 24 | 16 | 8 |
| 30 | 32 | 16 |
| 36 | 64 | 32 |
| 42 | 64 | 0 |
Nun kannst du die Aufgaben lösen.
a) Der Teich hat eine Gesamtfläche von 64 m². Diese Fläche ist ab dem 36. Tag vollständig bedeckt. Das liest du in der 7. Zeile ab.
b) Der Besitzer schafft es innerhalb von 6 Tagen nur 8 m² Seerosen zu entfernen. Ab dem 24. Tag vergrößert sich aber die Zunahme der Fläche auf mehr als 8 m² innerhalb von 6 Tagen. Also kann er ab dem 24. Tag den Teich nicht mehr von Seerosen befreien.
Oft hilft es, eine Wertetabelle anzulegen. Dann hast du eine Übersicht über die Funktionswerte.
Hier im Beispiel: Du berechnest die Tabelleneinträge zunächst mit den Informationen aus der Aufgabe (Verdopplung der Fläche alle 6 Tage). Damit hast du die Tageseinträge (jeweils 6er-Schritte) und die Funktionswerte (1,2,4, usw.).
Wirkungsdauer von Medikamenten
Ein Kind hat starke Schmerzen, weil es sich verbrannt hat. Zur Linderung soll es einen Schmerzsaft einnehmen. Beim ersten Mal soll das Kind 2 ml schlucken, ab dem 2. Mal nur noch 1,4 ml. Das Medikament wird im Körper so abgebaut, dass nach 4 Stunden noch 55 % des Medikaments vorhanden sind und wirken können.
a) Das Kind spürt die Schmerzen wieder, wenn nur noch 0,6 ml im Körper vorhanden sind. Bleibt das Kind schmerzfrei, wenn es alle 8 Stunden das Medikament einnimmt?
b) Damit die Dosis immer gleich hoch bleibt, sollen nach 8 Stunden nur noch 1,4 ml und nicht 2 ml aufgenommen werden. Warum ist das so? Begründe deine Antwort.
Lösung
Stelle die Wertetabelle über die Medikamentendosis im Körper auf.
Berechne zuerst 55 % von 2 ml. Das ist der Wert der Dosis nach 4 Stunden:
2 ml⋅55100=1,1 ml.
Der Wert nach 8 Stunden: Berechne 55 % von 1,1 ml.
1,1 ml⋅55100=0,605 ml
0,605 ml⋅55100=0,33275 ml.
Also:
| Zeit in Stunden | 0 | 4 | 8 | 12 |
| Medikamentendosis in ml | 2 | 1,1 | 0,605 | 0,33275 |
a)
Aus der Tabelle kannst du ablesen, dass nach 8 Stunden noch 0,605 ml im Körper vorhanden sind. Das sind mehr als 0,6 ml. Das Kind spürt also nach 8 Stunden noch keine Schmerzen.
b)
Da im Körper nach 8 Stunden noch 0,605 ml vorhanden sind, genügt es, 1,4 ml aufzunehmen. Denn 1,4 ml + 0,605 ml = 2,005 ml. Damit sind im Körper wieder rund 2 ml vorhanden. So kommt es zu keiner großen Überdosierung.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen