Lineares und quadratisches Wachstum
Mit dem Fahrrad an die Ostsee
Paul und Tam fahren gemeinsam mit dem Fahrrad an die Ostsee. Tam hat für die Reise extra einen neuen Fahrradcomputer gekauft. Dieser zeigt ihr die Durchschnittsgeschwindigkeit von 15kmh an. Sie sagt zu Paul: „Nun sind wir schon 45 km gefahren. Behalten wir unsere Durchschnittsgeschwindigkeit bei, so haben wir die verbleibenden 60 km in 4 Stunden geschafft.“ Paul meint dazu: „Unsere zurückgelegte Strecke nimmt bei gleichbleibender Geschwindigkeit pro Zeiteinheit immer um die selbe Entfernung zu.“
Nimmt in gleichen Abschnitten ein abhängiger Wert (Funktionswert) immer um die gleiche Menge zu, so heißt diese Zunahme lineares Wachstum.

Berg- und Talfahrt
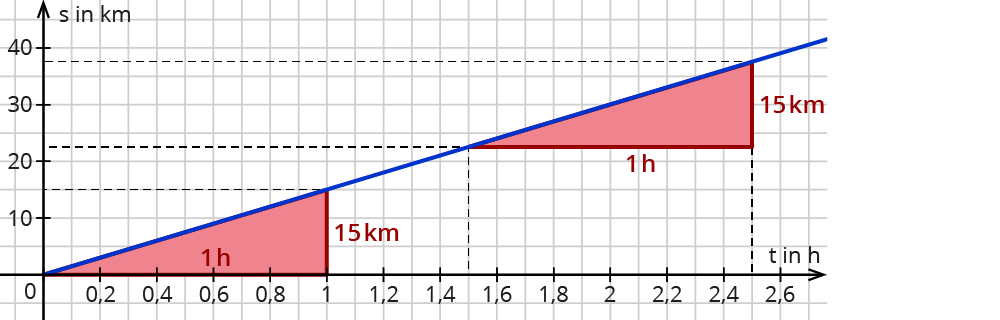
Auf dem Fahrradcomputer kann Tam sehen, welche Strecke sie in welcher Zeit zurücklegt.

Die Steigung der Geraden gibt an, wie viel Weg in einer Zeitspanne geschafft wird. Die Steigung ist hier also die Geschwindigkeit.
Die Steigung ist an allen Stellen gleich groß.
m=15km-0km1h-0h=15kmh
m=y2-y1x2-x1
Der Weg, der mit einer Geschwindigkeit von 15kmh zurückgelegt wurde, verläuft als gleichmäßig steigende Gerade.
Beim linearen Wachstum entsteht eine Gerade mit einer festen Steigung.
Bei gleichen Zeitspannen nimmt der Weg um den gleichen Betrag zu. Das siehst du auch an der Tabelle:

Da später auch andere Funktionen hinzukommen und man nicht immer einen Graphen zeichnet, spricht man allgemein von Änderungsraten.
Unter einer Änderungsrate oder Wachstumsgeschwindigkeit versteht man die Menge, die zwischen zwei Zeiteinheiten oder Argumenten einer Funktion hinzukommt.
Bei linearem Wachstum ist die Änderungsrate immer gleich groß.
Funktionswert und Funktionsgleichung, was war das nochmal?
Paul und Tams von der Zeit abhängiger Wert ist die zurückgelegte Strecke. Sie ändert sich pro Zeit. Für jeden festen Zeitpunkt kann dieser im Vorhinein berechnet werden.
Das klingt doch nach einer Funktion? Genau. Lineares Wachstum kannst du als lineare Funktion darstellen. Eine lineare Funktion hat als Funktionsgleichung die Form f(t)=m⋅t+b .
Hier ist die Variable t, weil die Strecke von der Zeit (t) abhängt.
Pro Zeiteinheit einer Stunde nimmt die Strecke um 15 km zu. Damit wissen wir m=15kmh.
Für die Berechnung ab dem Gesprächszeitpunkt benötigt man noch die Strecke, die sie bis dahin gefahren sind: s=45km.
Damit lässt sich die Funktionsgleichung aufstellen:
s(t)=15kmh⋅t+45km
Wie weit sind sie nun nach weiteren 2 Stunden gefahren?
s(2)=15kmh⋅2h+45km
s(2)=75km
Sie sind nach 2 Stunden 75 km weit gefahren.
Lineares Wachstum kannst du mithilfe der Funktionsgleichung für lineare Funktionen darstellen:f(x)=m⋅x+b.
Hängt die Größe von der Zeit ab, findest du als Variable meist t. f(t)=m⋅t+b.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Wie kann man die lineare Änderung berechnen?
| Zeit in h | 0 | 4 | 2 |
|---|---|---|---|
| Zurückgelegte Strecke s in km | 45 | 60 | 75 |
Für die Änderungsrate der Strecke kann man rechnen:
m=Zurückgelegte Strecke 2-zurückgelegte Strecke 1Zeit zur Strecke 2-Zeit zur Strecke 1
m=75km-60km2h-1h=15km1h=15kmh
Dies ist auch unabhängig von den gewählten Einträgen:
m=75km-45km2h-0h=30km2h=15kmh
Beim linearen Wachstum kann man die Änderungsrate mit der Formel für die Steigung berechnen:
m=y2-y1x2-x1
Erkennt man in einer Tabelle, dass in gleichen Zeiten oder in gleichen Abschnitten stets die Werte um den selben Wert zunehmen, so spricht man vom linearen Wachstum. Dies kann man mit der Gleichung unten rechnerisch prüfen.
Wie geht es eigentlich Paul und Tam inzwischen?
Paul und Tam sind an der Ostsee angekommen und liegen am Strand. Paul baut am Strand eine Burg. Für die ersten 10 cm Höhe benötigt Paul 1 min. Um die Burg auf 20 cm Höhe zu bekommen, benötigt er insgesamt 4 min.

Eine Tabelle zeigt den Zusammenhang zwischen Höhe und Zeit:

Tam erkennt hier die Quadratzahlen. Die Zeit für den Bau der Burg lässt sich nun nicht mit der Formel für das lineare Wachstum beschreiben.
Die Quadratzahlen kannst du so schreiben: t(h)=h2
Der Graph sieht so aus:

Neben dem linearen Wachstum gibt es auch andere Wachstumsarten wie das quadratische Wachstum. Quadratisches Wachstum kannst du mithilfe der Funktionsgleichung für quadratische Funktionen darstellen:f(x)=a⋅x2+bx+c.
Beim quadratischen Wachstum verändert sich die Steigung oder Änderungsrate. (hier: +1, +3, +5, …)
Sie schrumpft oder wächst proportional.
Vergeht die Zeit schneller, wenn’s schön ist?
oder: lineare Abnahme
Tam und Paul sitzen beim letzten Abendessen in ihrem Urlaub bei Kerzenschein am Tisch. Als sie ein letztes mal die Stille genießen, fällt Tam auf, dass die Kerze, auf die sie blickt, gleichmäßig kürzer wird. Sie ist so vertieft darin, dass sie auf die Serviette folgende Tabelle schreibt:

Sie stellt fest, es handelt sich wieder um eine lineare Änderung.
Wann muss der Kellner eine neue Kerze bringen?
Sie erkennt folgende Funktionsgleichung: h(t)=15cm-1cm5min⋅t oder h(t)=-1cm5min⋅t+15cm
Die Kerze ist bei 0 cm Höhe abgebrannt. Wann also ist h(t) gleich 0?
0=-1cm5min⋅t+15cm ∣ -15cm
-15cm=-1cm5cm⋅t ∣ :(-1cm5min)
75min=t
Erst in 75 min muss der Kellner die Kerze austauschen.

Es gibt nicht nur lineare Wachstums-, sondern auch Abnahmeprozesse. Dann ist in der Funktionsgleichung f(x)=mx+b die Steigung m negativ.

Eine lineare Wachstumsfunktion kann mit Hilfe ihres Anfangswertes und ihrer Änderungsrate leicht aufgestellt werden. Der Anfangswert ist der Wert zum Argument 0. Die Änderungsrate kann man mit der Formel der Steigung bestimmen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Regenabend
Es regnet nun schon den ganzen Tag. Paul ist schlecht gelaunt. Er schnappt sich ein quadratisches Blatt 8 cm x 8 cm Papier und beginnt in der Ecke einen Streifen abzuschneiden. Er schneidet jeweils nach 1 cm ein. Anschließend schneidet er im Abstand von 2 cm wieder ein. Dies wiederholt er fortlaufend. Das Blatt verkleinert sich vom Flächeninhalt so jeweils immer. Beim ersten Streifen verkleinert sich der Flächeninhalt des Blattes um 1 cm².


Plötzlich stellt er fest: „Hier sind auch wieder Quadratzahlen versteckt.“ Denn
64cm2-12cm2=63cm2,
64cm2-22cm2=60cm2,
64cm2-32cm2=55cm2,
Als Funktionsgleichung:
A(x)=64-x2
A ist die verbleibende Papiergröße und x der Einschnitt nach cm.
Von einer bestehenden Größe werden Vielfache der Quadratzahlen der Argumente abgezogen.

Es gibt auch quadratische Abnahmeprozesse. Dann ist in der Funktionsgleichung f(x)=ax2+bx+x der Parameter a negativ.
Der Funktionsgraph ist eine nach unten geöffnete Parabel.
Zusammenfassung
Hier hast du alles auf einen Blick über Wachstums- und Abnahmeprozesse.
| Name | lineares Wachstum oder Abnahme | quadratisches Wachstum oder Abnahme |
|---|---|---|
| Eigenschaft | Zahlenwerte ändern sich proportional zum Argument | Zahlenwerte ändern sich quadratisch zum Argument |
| Funktion | f(x)=m⋅x+b | f(x)=ax2+bx+c a≠0 |
| Änderungsrate | fest | ändert sich |
| Wachstum oder Abnahme | m>0 Wachstum, m<0 Abnahme | a>0 Wachstum, a<0 Abnahme |
| Funktionsgraph | Gerade | Parabel |
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen