Ganzrationale Funktionen untersuchen (Symmetrien, Globalverlauf)
Ganzrationale Funktionen untersuchen
Wie können wir ganzrationale Funktionen unterscheiden und beschreiben? Dazu betrachten wir ihre Globalverlauf und eventuelle Symmetrien.
Globalverlauf
Eine ganzrationale Funktion hat die Standardform $$f(x) = a_nx^n+a_(n-1)x^(n-1)+cdots+a_1x+a_0$$ ($$n$$$$in$$$$NN$$, $$a_i in RR$$ , $$a_n !=0)$$. Der Funktionsterm setzt sich aus Potenzfunktionen zusammen. Wir bezeichnen ihn oft auch als Polynom vom Grad $$n$$. Die $$a_i$$ heißen Koeffizienten von $$f$$.
Unter dem Globalverlauf einer ganzrationalen Funktion verstehen wir den Verlauf der Funktionswerte im Unendlichen, also
$$f(x) rarr oo $$ für $$ x rarr +- oo $$.
Beispiele für ganzrationale Funktionen
Hier siehst Du Beispiele einiger ganzrationaler Funktionen:
| $$f(x) = 3x-5$$ | ganzrationale Funktion - Grad 1 |
| $$g(x) = 5x^2+8x-3$$ | ganzrationale Funktion - Grad 2 |
| $$h(x) = 3x^4+7x^3-8x^2+x-9$$ | ganzrationale Funktion - Grad 4 |
Gegenbeispiele
Die nachfolgenden Beispiele sind keine ganzrationalen Funktionen:
| $$k(x) = x^3 + sqrt(x)$$ | $$sqrt(x) $$ ist nicht als $$x^n$$ mit $$n in NN$$ zu notieren |
| $$m(x) = 3xy -2z + 8$$ | $$m$$ enthält 3 Variablen |
| $$n(x) = 5x + (1/x) -13 $$ | $$(1/x)$$ ist nicht als $$x^n$$ mit $$n in NN$$ zu notieren |
Wichtige Größen bei ganzrationalen Funktionen sind ihr Grad und der Koeffizient der höchsten Potenz. Hier siehst Du ein paar Beispiele, wie Du sie ablesen kannst.
| ganzrationale Funktion | Grad | Koeffizient der höchsten Potenz |
|---|---|---|
| $$f(x) = 4x - 8$$ | 1 | $$4$$ |
| $$g(x) = 2x - 5x^2 + 3 $$ | 2 | $$ -5 $$ |
| $$h(x) = a_3x^3 + a_2x^2 + a_0$$ | 3 | $$a_3$$ |
.
Unterschiedliche Globalverläufe von ganzrationalen Funktionen
Es lässt sich folgender Satz zeigen:
Bei einer ganzrationalen Funktion $$f(x)$$ in der Standardform entscheidet der Term mit der höchsten Potenz von $$x$$ über den Globalverlauf von $$f$$.
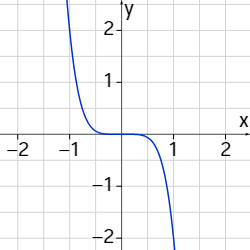
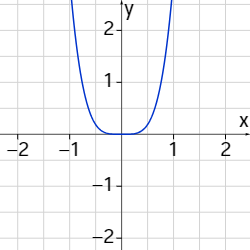
Somit erhalten wir vier mögliche Globalverläufe, zu denen Du jeweils eine Beispielfunktion abgebildet siehst.
Fall: $$n$$ ungerade, $$a_n > 0$$
Fall: $$n$$ ungerade, $$a_n < 0$$
Fall: $$n$$ gerade, $$a_n > 0$$
Fall: $$n$$ gerade, $$a_n < 0$$
Unter dem Globalverlauf einer ganzrationalen Funktion verstehen wir den Verlauf der Funktionswerte im Unendlichen, also
$$f(x) rarr oo $$ für $$ x rarr +- oo $$.
Symmetrie
Ganzrationale Funktionen können auch Symmetrien aufweisen. Hier können wir zwei Fälle unterscheiden:
Hat eine ganzrationale Funktion $$f$$ in der Standardform nur gerade natürliche Exponenten (der Potenzen von $$x$$), so verläuft der Graph von $$f$$ achsensymmetrisch zur y-Achse. Für alle$$x$$ gilt $$f(-x)=f(x)$$.
Enthält die Standardform nur ungerade natürliche Exponenten (der Potenzen von $$x$$), so ist verläuft der Graph punktsymmetrisch zum Koordinatenursprung $$O(0|0)$$. Für alle$$x$$ gilt $$f(-x)=-f(x)$$.
Beispiel 1
Die Funktion $$f()=x^4 -3x^2+1$$ ist achsensymmtrisch zur y-Achse:
Nachweis: $$f(-x) = (-x)^4 -3(-x)^2 +1 =x^4 -3x^2+1=f(x)$$
Beispiel 2
Die Funktion $$f(x)=x^5-3x$$ ist punktsymmetrisch zum Koordinatenursprung:
Nachweis: $$f(-x) = (-x)^5 -3(-x) =-x^5 +3x=-(x^5-3x)=-f(x)$$
Ganzrationale Funktionen können natürlich auch keine Symmetrien aufweisen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
