Nullstellen ganzrationaler Funktionen bestimmen

Mathematik

Deutsch

Englisch

kapiert.de kann mehr!

Nullstellen ganzrationaler Funktionen bestimmen

Damit Du die Nullstellen ganzrationaler Funktionen finden kannst, gibt es verschiedene Ansätze. Wir fangen mit den Funktionen mit niedrigstem Grad an.

Nullstellen linearer und quadratischer Funktionen

Die einfachste ganzrationale Funktion ist die lineare Funktion wie zum Beispiel

$f(x) = 2x - 6$ .

Nullstellen ganzrationaler Funktionen bestimmen

Ist $x_0$ eine Nullstelle von $f(x)$ , dann muss gelten: $f(x_0)=0$ , also

$2x_0 - 6=0$

$hArr$ $2x_0 = 6$ $hArr$ $x_0=3$

Somit hat $f$ bei $x_0=3$ eine Nullstelle.

Eine ganzrationale Funktion 2. Grades ist eine quadratische Funktion wie

$g(x) = x^2 + x - 2$

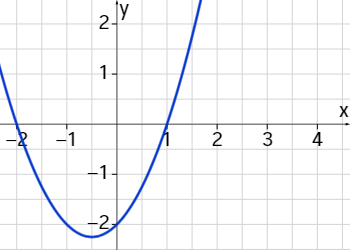
Nullstellen ganzrationaler Funktionen bestimmen

Hier kannst Du die p-q-Formel nutzen:

Ansatz: $x_0^2 + x_0-2=0$

Die Gleichung $x^2+px+q = 0$ hat die Lösungen $x_1,2 =-(p/2)+-sqrt((p^2/4)-q$ .

Mit $p=1, q=-2$ erhältst du $x_1 =-1/2+sqrt(1/4+2)=-1/2+ sqrt(9/4)=-1/2+3/2=1$ und $x_2 =-1/2-sqrt(1/4+2)=-1/2- sqrt(9/4)=-1/2-3/2=-2$

Oder Du nutzt die a-b-c-Formel:

Die Gleichung $ax^2+bx+c =0$ mit $a+-0$ hat die Lösungen

$x_1,2 =(-b+-sqrt(b^2-4ac))/(2a)$ .

Mit $a =1, b=1, c=-2$ erhältst du

$x_1 =(-1+sqrt(1-4*1*(-2)))/(2) =(-1+sqrt(9))/2=1$ und $x_2 =(-1-sqrt(1-4*1*(-2)))/(2) =(-1-sqrt(9))/2=-2$ .

((Grafik einfügen: 3_18_3_VE-1)) ((Grafik einfügen: 3_18_3_VE-2))

Nullstellen ganzrationaler Funktionen höheren Grades

Haben die ganzrationalen Funktionen einen Grad größer als $2$ , kann das Finden von Nullstellen schwieriger sein. Wir nehmen einmal an, dass es eine ganzzahlige Nullstelle gibt. Schau Dir dazu diese Funktion an:

(3) $f(x)=x^3 - x^2-4x+4$

Mit ein wenig Probieren oder Raten kannst du vielleicht auf die Nullstelle $x_0 = 1$ kommen, denn es gilt $f(1) = 13 - 12 - 4 + 4 = 0$ .

Damit hast du einen Linearfaktor, hier $(x_0 - 1)$ gefunden. Nun kannst du einen wichtigen Satz anwenden:

Du findest die Funktion $g$ durch eine Polynomdivision: $f(x) : (x-1) = g(x)$ , die hier noch einmal an der Beispielaufgabe wiederholt werden soll.

Polynomdivision

Nullstellen ganzrationaler Funktionen bestimmen

Damit folgt $f(x)=(x-1)*(x^2-4)=(x-1)*(x+2)*(x-2)$ . Als Nullstellen erhalten wir: $x_1=-2, x_2=1$ und $x_3= 2$ .

Nullstellen ganzrationaler Funktionen bestimmen

Ist $x_0$ eine Nullstelle der ganzrationalen Funktion $f$ , dann gilt: $f(x)=(x-x_0)*g(x)$ , wobei $g$ eine ganzrationale Funktion mit einem Grad kleiner ist als der von f.

Schlussfolgerungen

Was kannst Du allgemein daran erkennen?

Ist $f$ eine ganzrationale Funktion in der Standardform mit allen $a_i$ ganzzahlig und $a_0!= 0$ , so sind die ganzzahligen Nullstellen von $f$ immer Teiler von $a_0$ .
Ist $x_0$ eine Nullstelle von $f$ , so gilt $f(x) = (x - x_0) * g(x)$ . Der Grad von $g$ ist um $1$ kleiner als der von $f$ .

Weiteres Beispiel:

Bei $f(x) = x^3(x-1)^2$ ist $x_1 = 0$ eine dreifache und $x_2 = 1$ eine zweifache Nullstelle.

Allgemein gilt: Eine ganzrationale Funktion mit dem Grad $n$ hat maximal n Nullstellen, dabei werden mehrfache Nullstellen auch mehrfach gezählt.

Kannst du aus $f(x)$ den Faktor $(x - x_0)$ mehrfach ausklammern, so wird $x_0$ als mehrfache Nullstelle bezeichnet.

Nullstellen einer Funktion in der biquadratischen Form

Manchmal lassen sich auch Funktionen höheren Grades mit den bekannten Ansätzen für quadratische Gleichungen lösen. Schau Dir dazu diese Funktion an:

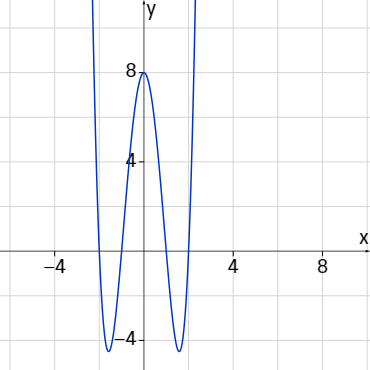
$f(x)=2x^4-10x^2+8$

Wenn Du diese Funktion gleich Null setzt und durch $2$ teilst, wird aus

$2x^4 -10x^2+8=0$

die Gleichung

$x^4-5x^2+4=0$ .

Nun kannst du substituieren, das heißt Du ersetzt das $x^2$ durch eine anders genannte Variable: $x^2 = u$ . Damit folgt eine Gleichung , die du jetzt mit der p-q-Formel lösen kannst:

$u^2-5u+4=0$ .

Rechne nun selbst: Mit $p=-5$ und $q = 4$ erhältst du $u_1=4$ und $u_2=1.$

Jetzt musst Du dies noch zurück substituieren: aus $x^2=u$ folgt $x=\pm\sqrt(u)$ . Du erhältst hier also die vier Nullstellen $x_1,2 =+-2$ und $x_3,4 = +-1$ .