Mit den Begriffen Steigung, Änderungsrate und Ableitung umgehen
Steigung
Bist Du schon einmal auf einer Straße in den Bergen gefahren und hast ein solches Schild gesehen?
Dies bedeutet, dass auf der nachfolgenden Strecke eine Steigung von 12% zu erwarten ist. Das heißt, pro 100 m die zurückgelegt werden, wird eine Höhe von 12 m überwunden:
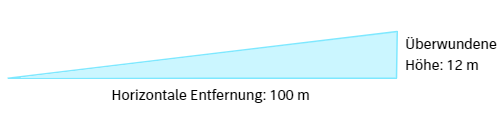
Tangentensteigung und Ableitung
Blicke noch einmal kurz auf die Straße im ersten Bild der ersten Seite. Eine Straße hat ja nicht nur auf ihrer ganzen Länge eine konstante Steigung bzw. Gefälle. Sie hat ein Profil, das wie die Kurve in der Abbildung aussieht:
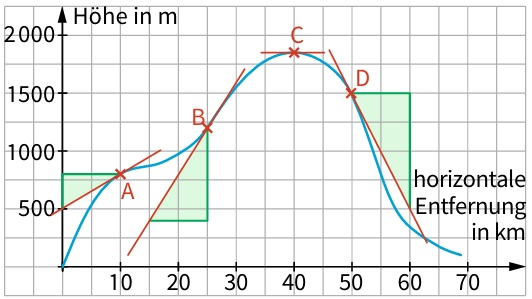
In der Abbildung siehst du drei Steigungsdreiecke eingezeichnet: zwei mit positiver Steigung und eines mit Gefälle, also negativer Steigung. Hier kannst du sogar die Steigungen direkt ausrechnen:
Steigung im Punkt A: 800 m-500 m10 km=0,03=3%,
im Punkt B: 8% und im Punkt D:-10%.
Beachte, dass im Punkt C die Steigung auf waagerechter Strecke 0% oder einfach 0 ist.
In der Abbilddung siehst du noch etwas: es sind die Tangenten durch die angegebenen Punkte. Sie entsprechen auf Grund ihrer Eigenschaft der Steigung des Graphen im jeweiligen Punkt.
Die Steigung m eines Graphen einer Funktion f an einer Stelle x ist die Steigung der Tangente in diesem Punkt P(x∣f(x)).
Diese Tangentensteigung m wird auch als Ableitung der Funktion an der Stelle x bezeichnet und wir schreiben m=f‘(x).
Ableitung
Das Anlegen einer Tangente an einen Graphen in einem Punkt P zur genauen Bestimmung der Steigung in P ist mathematisch nicht exakt, da sie nach Augenmaß eingezeichnet wird. Daher wird ein Verfahren genutzt, das mit einer Tangente arbeitet, die als Grenzgerade von Sekanten entsteht.
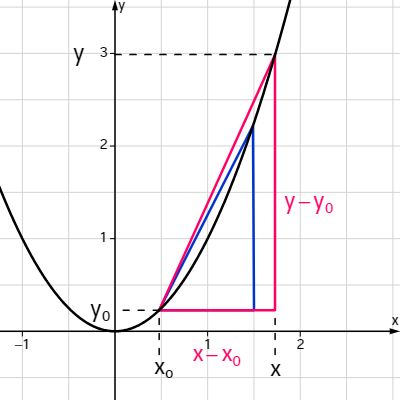
Die Sekante durch die Punkte P(x0∣f(x0)) und Q(x∣f(x)) hat die Steigung m=y-y0x-x0=f(x)-f(x0)x-x0. Je näher der Punkt Q zum Punkt P wandert, desto weniger unterscheidet sich die Sekante von der Tangente am Punkt P. Mathematisch notieren wir dies durch einen Grenzprozess
limx→x0f(x)-f(x0)x-x0.
Wir können nun die Tangentensteigung im Punkt P direkt berechnen:
limx→0,5x2-0,25x-0,5=limx→0,5(x-0,5)(x+0,5)x-0,5=limx→0,5(x+0,5)=1.
Damit können wir allgemein die Ableitung der Funktion f(x)=x2 an der Stelle x=0,5 mit f′(0,5)=1 angeben.
m=f(x)-f(x0)x-x0 bezeichnen wir als Differenzenquotient und f′(x0)=limx→x0f(x)-f(x0)x-x0 als Differentialquotient.
Die Tangentensteigung an den Graphen von f in einem Punkt P(x∣f(x)) heißt auch Ableitung der Funktion f an einer Stelle x .
Dafür wird auch f′(x) notiert.
Änderungsrate
Die hier dargestellten Überlegungen treten auch in vielen Anwendungssituationen auf. So unterscheiden wir z.B. zwischen Momentan- und Durchschnittsgeschwindigkeit.
Bei einer Geschwindigkeitsmessung der Polizei ist die Momentangeschwindigkeit von Interesse. Beim Überschreiten einer festgelegten Höchstgeschwindigkeit wird dann eine Strafe verhängt.
Die Durchschnittsgeschwindigkeit eines Autofahrers auf einem Streckenabschnitt ist in diesem Fall uninteressant.
Ein anderes Beispiel ist die Temperaturänderung beim Wasserkochen: wird die Temperatur des Wassers in einem Wasserkocher gemessen und damit ein Zeit-Temperatur-Diagramm erstellt, so lässt sich die Temperatur bei einer bestimmten Zeit als momentane Änderungsrate ablesen. Wird die Temperatur im Intervall zwischen 40° C und 90° C betrachtet, so kann aus der mittleren Änderungsrate über diesem Intervall abgelesen werden, ob die Temperatur linear ansteigt oder nicht.
Bei Anwendungen unterscheiden wir bei einer Funktion f zwischen einer Sekantensteigung auf einem Intervall [x0∣x] mit
ms=f(x)-f(x0)x-x0,
die wir als mittlere Änderungsrate bezeichnen und der Tangentensteigung
mt=limx→x0ms=limx→x0f(x)-f(x0)x-x0,
die wir momentane Änderungsrate nennen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen


