Näherungsverfahren

In der Mathematik dienen Näherungsverfahren dazu, ein Problem, das mit üblichen Verfahren nicht exakt gelöst werden kann, näherungsweise zu lösen. Das bedeutet dass man einen Weg sucht, eine ungefähre Lösung des Problems zu finden, die für die jeweilige Aufgabe ausreichend ist.

Als Beispiel kannst Du Dir die Bestimmung von $$sqrt 2$$ anschauen:
Du suchst eine Zahl $$a$$ für die gilt: $$a^2=2$$.

Diese Zahl muss zwischen $$1$$ und $$2$$ liegen muss, da gilt
$$1^2 = 1 < 2$$ und $$2^2 = 4 > 2$$ .

Jetzt kannst Du dieses Intervall $$[1 | 2 ]$$ halbieren und prüfst den Wert $$1,5$$, für den gilt: $$1,5^2=2,25 >2$$. Die gesuchte Zahl $$a=\sqrt 2$$ liegt also im Intervall $$[1|1,5]$$.

Du kannst jetzt entweder wieder das Intervall halbieren oder, um die erste Dezimalzahl herauszufinden, die Zahl $$1,4$$ ausprobieren. Für diese gilt $$1,4^2=1,96<2$$, also ist die erste Ziffer nach dem Komma eine $$4$$ und die gesuchte Zahl liegt im Intervall $$[1,4|1,5]$$.

So kannst Du jetzt weiter vorgehen und kommst auf das Intervall $$[1,41 | 1,42]$$, denn es gilt

$$1,41^2 = 1,9881 < 2$$ und $$1,42^2 = 2,0164 > 2$$.

Diese Methode kann unendlich oft fortgeführt werden - da $$\sqrt 2$$ eine irrationale Zahl ist, wirst du jedoch niemals zum Ende kommen.

In der Praxis reicht es, einen Näherungswert für $$sqrt2$$ zu wählen, der für das zugrunde liegende Problem ausreicht. In der Schule reicht es oft, mit $$sqrt2 ≈ 1,414$$ zu rechnen.

Näherungsverfahren - geometrisch

Näherungsverfahren gibt es nicht nur für algebraische Probleme, sondern auch für geometrische Probleme.

Ein Beispiel siehst Du hier: in einem Quadrat der Kantenlänge $$1$$ soll in jedem Schritt die Hälfte der noch ungefärbten Fläche eingefärbt werden.

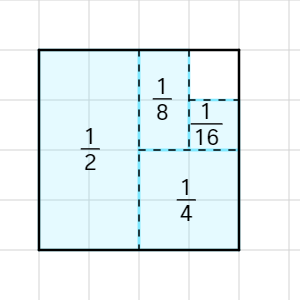
Wir möchten dies in einer Formel darstellen und bezeichnen den Anteil der gefärbten Fläche im $$n$$-ten Schritt mit $$s(n)$$.

Im ersten Schritt wird also die Hälfte des Quadrats gefärbt:
$$s(1) = 1/2 = 0,5$$
Im zweiten Schritt kommt die Hälfte der ungefärbten Hälfte, also ein Viertel, dazu:
$$s(2) = 0,5 + 1/4 = 0,75$$
Im Dritten Schritt kommt die Hälfte des freien Viertels, also ein Achtel, dazu:
$$s(3) = 0,75 + 1/8 = 0,75 + 0,125 = 0,875$$
Im nächsten Schritt folgt die Hälfte des ungefärbten Achtels, also ein Sechzehntel:
$$s(4) = 0,875 + 1/16 = 0,875 + 0,0625 = 0,9375$$

Daraus kannst Du auch eine allgemeine Formel aufstellen die so aussehen kann:
$$s(n) = s(n-1) + 1/(2^n)$$
Du kannst hier sehen, dass sich der Anteil der gefärbten Fläche immer mehr dem Wert $$1$$ annähert.

Näherungsverfahren - rekursiv und explizit

So wie wir diese Vorschrift zur Berechnung der Folge $$s(n)$$ aufgeschrieben haben, müssen wir immer den Wert des vorigen Schrittes kennen, um den nächsten zu berechnen. Dies kann etwas mühselig sein, wenn der Wert $$s(100)$$ gebraucht wird. Lässt sich der Wert vielleicht auch anders berechnen?

Wir wissen, dass die Summe den Wert $$1$$ nicht überschreiten kann - die Fläche ist ja auf $$1$$ begrenzt. Von daher können wir $$s(n)$$ auch so bestimmen, dass immer die noch freie Fläche vom Wert $$1$$ subtrahiert wird:
$$s(1) = 1 – 1/2 = 0,5$$
$$s(2) = 1 – 1/(2^2) = 1 – 1/4 = 0,75$$
$$s(3) = 1 – 1/(2^3) = 1 – 1/8 = 0,875$$

Auch dies können wir zu einer Formelzusammenfassen:
$$s(n) = 1 – 1/(2^n)$$.

Beide Darstellungen berechnen dasselbe - die erste Darstellung $$s(n)=s(n-1)-1/2^n$$ benötigt jedoch immer den Vorgängerwert der Folge. Solche Folgendarstellungen heißen rekursiv.

Berechnungsvorschriften von Folgen, die man „direkt“, also ohne Kenntnis eines oder mehrerer Vorgängerwerte bestimmen kann, heißen explizit.

Grenzwert

Aus der Betrachtung der beiden Darstellungsarten von Näherungswerten durch Folgen können wir eine weitere Eigenschaft feststellen: Die Werte der Folgenglieder nähern sich einem bestimmt Wert, den wir Grenzwertg nennen.

Definition

Wir betrachten die Glieder der Folge $$a(n)$$ mit $$a(n) = (n+2)/n$$ für wachsende Werte von $$n$$:

$$3 ; 2 ; 5/3 ; 6/4 ; 7/5 ; 4/3 ; … ; 12/10 ; …. $$

In einer Abbildung sieht dies folgendermaßen aus:

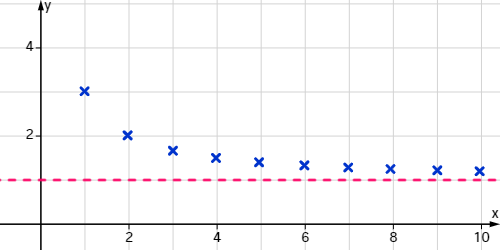
Wir vermuten, dass sich die Folgenglieder $$a(n)$$ mit wachsendem $$n$$ dem Grenzwert $$g = 1$$ nähern.
Wir schreiben dafür auch $$a(n) → 1$$ für $$n → ∞$$ oder
$$lim_{n\to\oo} a(n) = 1$$ .

Folgen, die einen Grenzwert $$g$$ besitzen, heißen konvergent.

Folgen ohne Grenzwert wie z.B. $$a(n) = 5^n$$ mit $$lim_{n\to\oo} a(n) = oo$$ heißen divergent.

Folgen, deren Glieder abwechselnd positiv und negativ sind, wie z.B. $$(-1)^n/n$$, heißen alternierend.

Der $$epsilon$$-Streifen

Aber was genau heißt es eigentlich, dass eine Folge einen Grenzwert $$g$$ besitzt? Dazu wird häufig der sogenannte $$\varepsilon$$-Streifen genutzt:

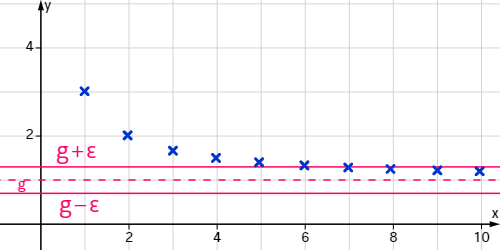
Wir legen um den Grenzwert $$g=1$$ einen Streifen der Breite $$2\varepsilon$$ um den Grenzwert.
Du siehst, dass von einem bestimmten $$n$$ an, die Folgenglieder innerhalb der $$epsilon$$-Umgebung von g liegen. Wenn es also ein $$n$$ gibt, von dem ab alle nachfolgenden Folgenglieder innerhalb der $$epsilon$$-Umgebung von $$g$$ liegen, dann wissen wir, dass wir tatsächlich den Grenzwert gefunden haben.

Wenn Du das konkret nachrechnen möchtest, sieht es so aus: wählen ein $$\varepsilon$$, z.B. $$epsilon = 0,2$$. Ab welchem $$n$$ liegen alle Werte der Folge $$s(n)=\frac{n+2}{n}=1+\frac{2}{n}$$ in der $$epsilon$$-Umgebung von $$g=1$$? Dazu kannst Du eine Gleichung aufstellen:

$$|s(n)-g|=|1-\frac{2}{n}-1|=|\frac{2}{n}|=\frac{2}{n}<0,2=\varepsilon$$

Stellst Du $$\frac{2}{n}<0,2$$ nach $$n$$ um, erhältst Du $$n>10$$, d.h. ab $$s(11)$$ liegen alle Werte in der $$0,2$$-Umgebung des Grenzwertes!

Bestimmung von Grenzwerten

Die Bestimmung von Folgengrenzwerten und deren Nachweis ist nicht immer einfach. Häufig hilft es, die Probleme umzuschreiben und auf bekannte Folgen zurückzuführen. Auch der Einsatz eines Computeralgebrasystems kann sehr hilfreich sein.

Beispiele

1. Folgen wie $$a(n) = 1/(5n)=\frac{1}{5}*\frac{1}{n}$$ oder $$a(n) = 1/(n^2)$$ lassen sich leicht auf eine Nullfolge $$\frac{1}{n}$$ zurückführen und sind daher konvergent mit g = 0 .
2. Die Folge $$a(n) = sqrt(2n)$$ ist divergent, da mit steigendem $$n$$ die Folgenglieder über alle Grenzen wachsen.
3. Bei gebrochen rationalen Folge hilft häufig der Trick, die höchste Potenz „herauszukürzen“:
   $$a(n) = (4n^2+3n)/(3n^2-2) = (4+3/n)/(3-2/n^2)$$
   Hier tauchen wieder die bekannten Nullfolgen $$3/n$$ und $$2/n^2$$ auf, so dass insgesamt gilt
   $$a(n) rarr 4/3$$ für $$n rarr oo$$.