Die Normalparabel untersuchen
Was ist die Quadratfunktion?
Wie der Name schon sagt, ordnet die Quadratfunktion f einer Zahl ihr Quadrat zu.
Das Quadrat von 2 ist 4, weil 22=2⋅2=4 ist.
Also ist f(2)=4.
Das Quadrat von 3 ist 9, weil 32=3⋅3=9 ist.
Also f(3)=9.
Für eine beliebige Zahl x bedeutet das:
Das Quadrat von x ist x2. Das heißt f(x)=x2.
Die Quadratfunktion f hat als Funktionsgleichung y=f(x)=x2.
Die Wertetabelle
Wie sieht der Graph der Quadratfunktion f aus?
Um den Graphen zeichnen zu können, berechnest du für viele verschiedene Zahlen die Funktionswerte.
Am besten legst du dafür eine Wertetabelle an:
| x | y=f(x)=x2 |
|---|---|
| -2 | 4 |
| -1 | 1 |
| -12 | 14 |
| -14 | 116 |
| 0 | 0 |
| 14 | 116 |
| 12 | 14 |
| 1 | 1 |
| 2 | 4 |
Graph der Quadratfunktion
Nun kannst du die Punkte aus der Wertetabelle in ein Koordinatensystem eintragen.
Wertetabelle
| x | y=f(x)=x2 |
|---|---|
| -2 | 4 |
| -1 | 1 |
| -12 | 14 |
| -14 | 116 |
| 0 | 0 |
| 14 | 116 |
| 12 | 14 |
| 1 | 1 |
| 2 | 4 |
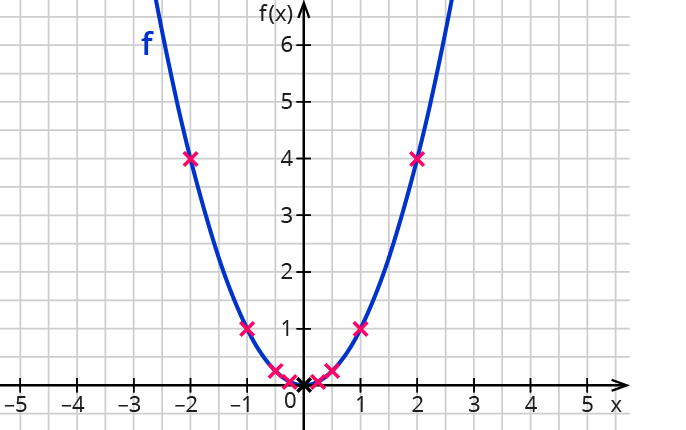
Graph im Koordinatensystem
Zeichne alle Punkte ein und verbinde sie.
Achtung: Die einzelnen Punkte liegen offensichtlich nicht auf einer Geraden. Du kannst die Punkte nicht mit einem Lineal verbinden.
Dafür kannst du die Punkte entweder mit der freien Hand verbinden oder mit einer Schablone.

Der Graph der Quadratfunktion heißt Normalparabel.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Die Eigenschaften der Normalparabel
Was fällt dir an dem Graphen auf?
1. Der Graph ist symmetrisch zur y-Achse
Wenn zwei Punkte den gleichen Abstand zur y-Achse haben, dann befinden sie sich auf der gleichen Höhe.
Die Normalparabel ist symmetrisch zur y-Achse.
Die y-Achse ist die Spiegelachse für die Normalparabel.

2. Der Graph geht nicht unter die x-Achse
Egal was du für x einsetzt, da die Zahl mit sich selbst multipliziert wird, ist das Ergebnis nie negativ. Alle Funktionswerte sind positiv oder 0. Das heißt f(x)≥0: Alle y-Werte sind größer als 0.
Das kannst du auch am Graphen sehen. Der Graph geht nicht unter die x-Achse.

3. Der Graph hat einen Tiefpunkt
Der tiefste Punkt ist der Punkt (0|0). Man nennt den tiefsten Punkt Tiefpunkt oder Minimum. Es gibt also keinen y-Wert, der kleiner ist als der y-Wert vom Tiefpunkt.


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
4. Der Graph wächst links und rechts immer weiter
Gehst du vom Tiefpunkt nach rechts, steigen die y-Werte unaufhörlich. Das bedeutet: wenn du die Zahl, die du quadrierst, immer größer wählst, wird auch ihr Quadrat größer.
Gehst du vom Tiefpunkt nach links, steigen die y-Werte ebenfalls unaufhörlich. Das heißt: wenn ich die Zahl, die ich quadriere, immer kleiner wähle, wird ihr Quadrat immer größer.
5. Der Graph hat einen Scheitelpunkt
Der Tiefpunkt (0|0) ist auch der Scheitelpunkt. Er ist der einzige Punkt, der auf Normalparabel und auf der Spiegelachse liegt.

Die Normalparabel
- ist symmterisch zur y-Achse
- geht nicht unter die x-Achse
- hat bei (0|0) einen Tiefpunkt und Scheitelpunkt
Die Normalparabel im Überblick
Die Quadratfunktion f hat als Funktionsgleichung
y=f(x)=x2.
Der Graph der Quadratfunktion heißt Normalparabel.
Eigenschaften der Normalparabel:
- Der Graph ist symmetrisch zur y-Achse.
- Der Graph geht nicht unter die x-Achse.
- Der Graph hat einen Tiefpunkt bei (0|0).
- Der Graph wächst links und rechts immer weiter.
- Der Graph hat einen Scheitelpunkt bei (0|0).


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen