Quadratische Funktionen beschreiben
Was ist eine quadratische Funktion?
Hier lernst du eine neue Sorte von Funktionen kennen:
Ganz übersichtlich
Quadratische Funktionen – die Funktionsgleichung
Quadratische Funktionen haben die Funktionsgleichung
y=f(x)=a⋅x2+b⋅x+c.
Für a, b, c kannst du alle Zahlen einsetzen. Achtung: a darf nicht 0 sein.
Quadratische Funktionen – eine Wertetabelle
Beispiel für y=f(x)=x2–2x+2 :
| x | y=f(x)=x2–2⋅x+2 |
|---|---|
| - 1 | 5 |
| 0 | 2 |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
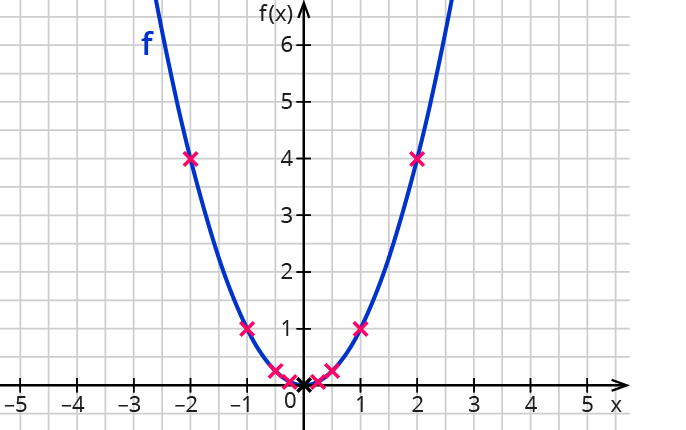
Quadratische Funktionen – der Graph
Der Graph einer quadratischen Funktion heißt Parabel.
Beispiel für y=f(x)=x2–2x+2 :

1. Beispiel
Funktionsgleichung: y=f(x)=x2–3
Die allgemeine Funktionsgleichung ist ja
y=f(x)=a⋅x2+b⋅x+c .
Also ist a=1, b=0 und c=–3 gewählt worden: y=f(x)=1⋅x2+0⋅x+(–3)=x2–3
Wertetabelle
Du berechnest die Werte für die ganzen Zahlen von -2 bis 2:
| x | y=f(x)=x2–3 |
|---|---|
| -2 | 1 |
| - 1 | -2 |
| 0 | -3 |
| 1 | -2 |
| 2 | 1 |
Der Graph: die Parabel


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
2. Beispiel
Funktionsgleichung: y=f(x)=–x2+x
Die allgemeine Funktionsgleichung ist ja
y=f(x)=a⋅x2+b⋅x+c .
Also ist a=–1, b=1 und c=0 gewählt worden: y=f(x)=(–1)⋅x2+1⋅x+0=–x2+x
Wertetabelle
Du berechnest die Werte für die ganzen Zahlen von -2 bis 2:
| x | y=f(x)=–x2+x |
|---|---|
| -2 | -6 |
| - 1 | -2 |
| 0 | 0 |
| 1 | 0 |
| 2 | -2 |
Der Graph: die Parabel

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen