Eine Funktion – zwei Schreibweisen

Die Funktionsgleichung für dieselbe Funktion kannst du in unterschiedlichen Formen aufschreiben.

Beispiele:

$$f (x) = x^2 -6x +8$$ ist die gleiche Funktion wie $$f (x) = (x-3)^2 -1$$.

Oder
$$g (x) = x^2 -x + 1,65$$ ist die gleiche Funktion wie $$ g(x) = (x -0,5)^2 + 1,4$$.

Keine Sorge, das siehst du auf den ersten Blick gar nicht. Da hilft nur nachrechnen.

Für $$f(x)$$:

Am einfachsten geht es, wenn du bei $$f (x) = (x-3)^2 -1$$ die Klammer auflöst.

$$f (x) = (x-3)^2 -1 $$
$$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$= x^2-2*3x +9-1$$
$$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$= x^2-6x +9-1$$
$$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$= x^2-6x + 8$$

Du siehst, die beiden Formen von $$f$$ stehen tatsächlich für die gleiche Funktion.

Und wie nennt sich das?

Die unterschiedlichen Darstellungen einer Funktion haben unterschiedliche Namen.

Die Darstellung der Funktion durch $$f(x) = x^2 - 6x + 8$$ heißt Normalform.

Aber wozu noch eine weitere Form?

An der zweiten Form $$f (x) = (x-3)^2 -1$$ kannst du ganz einfach Eigenschaften der Funktion ablesen. Ohne umständliches Zeichnen!

So sieht’s allgemein aus:

Eigenschaften von $$f (x) = (x-3)^2 -1$$

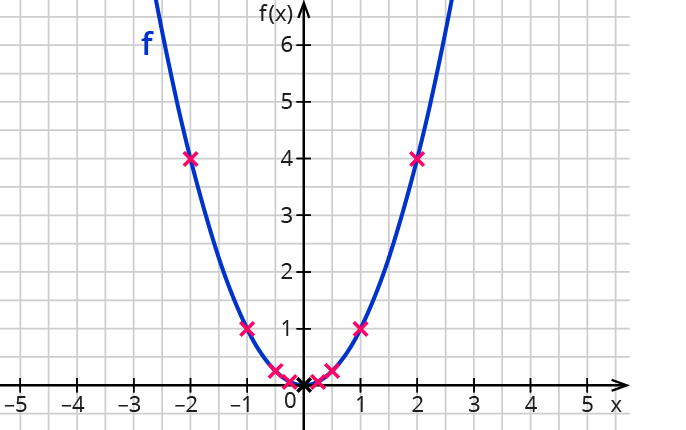
Der Graph der Funktion $$f$$ sieht so aus:

Welche Nullstellen hat $$f$$ ?

Die Nullstellen liegen bei $$(2|0)$$ und $$(4|0)$$.

Wo ist der Scheitelpunkt und Tiefpunkt von $$f$$ ?

Der Tiefpunkt und Scheitelpunkt ist $$(3|-1)$$.

Was hat $$f$$ als Wertebereich?

Der Wertebereich sind $$-1$$ und alle Zahlen, die größer sind.

Besitzt $$f$$ eine Symmetrieachse?

Ja, sie verläuft durch den Scheitelpunkt $$(3|-1)$$ und parallel zur $$y$$-Achse.

Ist dir aufgefallen, was du direkt aus dieser Funktionsgleichung $$f(x)= (x - 3)^2 - 1$$ ablesen kannst?

Den Scheitelpunkt! Deswegen heißt diese Funktion auch Scheitelpunktform.

Mit der Scheitelpunktform kennst du den Scheitelpunkt und zwar ohne eine Wertetabelle zu berechnen oder den Graphen zu zeichnen.

Beispiel: $$h(x) = (x + 0,5)^2 + 1,5$$

Das ist der Graph der Funktion $$h$$:

Wo ist der Scheitelpunkt und Tiefpunkt von $$h$$ ?

Der Tiefpunkt und Scheitelpunkt ist $$(-0,5|1,5)$$.

Was hat $$h$$ als Wertebereich?

Der Wertebereich sind $$1,5$$ und alle Zahlen, die größer sind.

Besitzt $$h$$ eine Symmetrieachse?

Die Spiegelachse verläuft durch den Scheitelpunkt $$(-0,5|1,5)$$ und parallel zur $$y$$-Achse.

Den Scheitelpunkt $$(-0,5|1,5)$$ kannst du wieder direkt aus der Funktionsgleichung $$h(x)= (x + 0,5)^2 +1,5$$ ablesen!

ACHTUNG:
Wenn du aus der Scheitelpunktform die $$x$$-Koordinate für den Scheitelpunkt schreibst, wechselt das Vorzeichen.
Aus $$+$$ wird $$-$$ und aus $$-$$ wird $$+$$.

In der Klammer steht $$+$$$$0,5$$. Daraus wird $$-$$$$0,5$$ im Scheitelpunkt.

Von der Normalform zur Scheitelpunktform

Die Scheitelpunktform ist oft viel praktischer. Wie kannst du eine Funktionsgleichung der Form $$f(x)= x^2 + px +q$$ umformen?

Dazu brauchst du die quadratische Ergänzung.

Suche für

$$f (x) = x^2 – 6x + 8$$

die Darstellung
$$f (x) = x^2 – 6x + 8$$
$$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$= (x - $$ $$)^2 +$$

1. Schritt: Suche $$b$$
Nach der Binomischen Formel muss in das erste graue Kästchen eine 3.

2. Schritt: Berechne $$b^2$$
Damit ergibt sich: $$ b^2 = 9$$

3. Schritt: Trick – addiere 0
Du darfst aber natürlich nicht eine 9 in eine Gleichung einfügen, deshalb gibt es jetzt einen Trick:
$$ + 9 – 9 = 0$$ und eine 0 darf du immer in einer Gleichung addieren:

4. Schritt: Berechne das zweite Kästchen
Daraus ergibt sich für das zweite Kästchen:

Also: $$f(x)=(x-3)^2-1$$

Fertig!
Nun hast du die Funktion von der Normalform in die Scheitelpunktform umgeformt!

Beispiel $$g(x)=x^2 + 3 x+1 $$

Suche für

$$g(x)=x^2 + 3 x+1 $$

die Darstellung
$$g(x)=x^2 + 3 x +1 $$
$$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$= (x +$$ $$)^2 + $$

1. Schritt: Suche $$b$$
Nach der Binomischen Formel muss in das erste graue Kästchen eine 1,5.

$$x^2+2bx+b^2$$

$$g(x) = x^2 + 3x$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$+ 1$$

$$= (x$$ $$+ 1,5$$ $$)^2 + $$

$$(x + b )^2 + $$

2. Schritt: Berechne $$b^2$$
Damit ergibt sich: $$ b^2 = 2,25$$

3. Schritt: Trick – addiere 0

$$ + 2,25 – 2,25 = 0$$ und eine 0 darf du immer in einer Gleichung addieren:

$$x^2+2bx+b^2$$

$$g (x) = x^2 + 3x$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$+ 1$$
$$g (x) = x^2 + 3x$$ $$+0$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$$$ $$+ 1$$
$$g(x) = x^2 + 3x$$ $$+ 2,25 -2,25$$ $$+1$$

$$= (x +1,5 )^2 -$$

$$(x + b )^2 + $$

4. Schritt: Berechne das zweite Kästchen
Daraus ergibt sich für das zweite Kästchen:

$$g (x) = x^2 + 3x+ 2,25 -2,25+1$$

$$= (x + 1,5 )^2$$ $$ -1,25$$

Also: $$g(x)=(x+1, 5)^2-1,25$$

Fertig!