Potenzfunktionen untersuchen
Was sind Potenzfunktionen?
Eine Potenzfunktion ist eine Funktion der folgenden Form:
f(x)=a⋅xb.
Dabei ist a eine beliebige reelle Zahl ungleich 0.
Die Zahl a heißt Koeffizient der Potenzfunktion.
Die Zahl b wird auch als Grad der Potenzfunktion bezeichnet.
Hier lernst du die Eigenschaften von Potenzfunktionen kennen.
Natürliche Zahlen ℕ: Das sind alle positiven ganzen Zahlen und die 0.
Reelle Zahlen ℝ: Das sind alle dir bekannten Zahlen.
Gerader Exponent
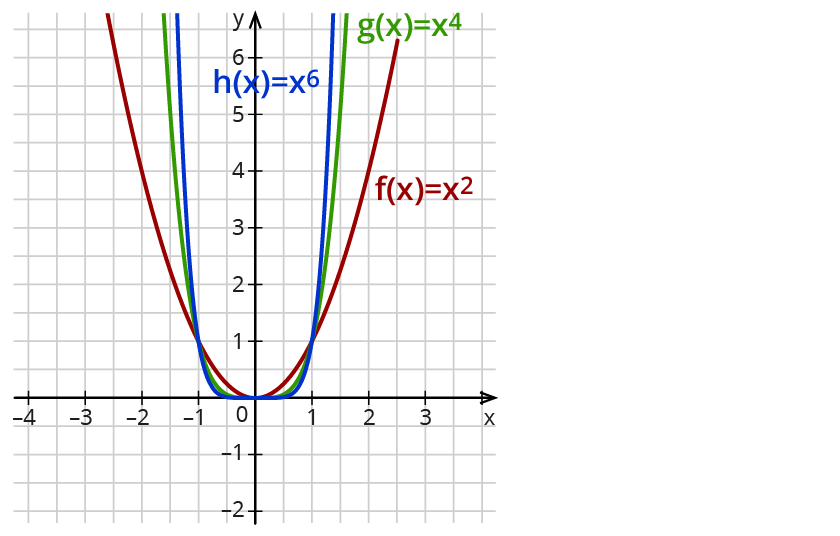
Die Graphen stehen stellvertretend für alle Graphen von Potenzfunktionen mit geradem Exponenten und positivem Koeffizienten a.
Du siehst:
Alle Graphen
- sind achsensymmetrisch zur y-Achse.
- verlaufen durch den gemeinsamen Punkt (0|0). x=0 ist die gemeinsame Nullstelle der Graphen.
- fallen für x≤0.
- steigen für x≥0.
In der Mathematik werden Eigenschaften von Funktionen häufig an ihren Graphen veranschaulicht.
Ungerader Exponent
Hier sind die Graphen von Potenzfunktionen mit ungeradem Exponenten und positivem Koeffizienten a.
Du siehst:
Alle Graphen
- sind punktsymmetrisch zum Ursprung.
- verlaufen durch den gemeinsamen Punkt (0|0).
- steigen für alle Werte von x.
Punktsymmetrisch bedeutet, dass die beiden Teile des Graphen durch eine Drehung um 180° ineinander übergehen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Der Koeffizient a
Welchen Einfluss hat nun das a in f(x)=a⋅xb?
In den Bildern wurde bei der Funktion f(x)=a⋅x2 nur der Wert von a variiert.
a positiva negativ
Du erkennst:
- a staucht oder streckt die Graphen in y-Richtung.
- Für a<0 sind die Graphen an der x-Achse gespiegelt.
Wenn du das gleiche für Funktionen mit ungeradem Exponenten wiederholst, erkennst du, dass der Parameter a hier genau so funktioniert.
a positiva negativ
- 0<a<1: Graph gestaucht
- 1<a: Graph gestreckt
- -1<a<0: Graph gestaucht und an der x-Achse gespiegelt
- a<-1: Graph gestreckt und an der x-Achse gespiegelt
Im Überblick
Was ist eine Potenzfunktion?
Funktion vom Typ f(x)=a⋅xb;
a: beliebige Zahl; b: natürliche Zahl; a und b nicht 0
Wie beeinflusst der Exponent b die Form des Graphen?
| gerader Exponent | ungerader Exponent | |
| Symmetrie | achsen- symmetrisch zur y-Achse | punktsymmetrisch (Drehung um 180°) zum Punkt (0|0) |
| Monotonie- verhalten | monoton fallend für x<0, monoton steigend für x>0* | monoton steigend* |
| gemeinsame Punkte | (0|0) | (0|0) |
*Diese Aussagen gelten jeweils für den Grundtypus, das heißt, wenn die Zahl a positiv ist. Ist a negativ, kehrt sich das Monotonieverhalten um.
Wie beeinflusst der Koeffizient a die Form des Graphen?
a staucht oder streckt die Graphen in y-Richtung.
Für negative Werte von a wird der Grundtyp des Graphen an der x-Achse gespiegelt.
Tabellenübersicht über die Gestalt der verschiedenen Graphen
Exponent geradeExponent ungerade


kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen