Anwendungsaufgaben mit Sinus- und Kosinusfunktion
Leben an der Küste
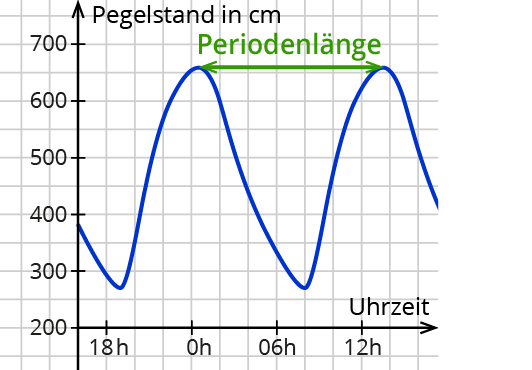
Kalle lebt im Dörfchen Deichblick an der Nordseeküste. Er misst an einem Tag jede Stunde den Wasserstand und trägt ihn in ein Koordinatensystem ein.
x-Achse: Zeit in Stunden
y-Achse: Wasserstand in m

Kalle hat seine eingetragenen Punkte verbunden: Wenn das nicht wie eine Sinusfunktion aussieht!
Die Sinusfunktion hat ja die allgemeine Gleichung f(x)=a⋅sin(b⋅(x-c))+d.
Kalle möchte die Parameter bestimmen. Dann könnte er für beliebige Zeitpunkte den Wasserstand berechnen (x einsetzen, y ausrechnen).
Jaaa, in der Realität sieht die Kurve natürlich nicht genau so aus.:-) Die Periodenlänge der Gezeiten ist eigentlich 12,44 Stunden. Daher verschieben sich die Gezeiten von Tag zu Tag um etwa eine Stunde nach hinten. Außer dem Stand des Mondes gibt es noch weitere Einflüsse. Aber trotzdem bleibt die Sinuskurve immer erkennbar.
 Bild: U. Muuß
Bild: U. Muuß
Menschen, die mit Ebbe und Flut leben, brauchen jeden Tag die Zeiten vom Hoch- und Tiefwasser. Das kann dann so aussehen:
 Bild: Günter Schmidt
Bild: Günter Schmidt
Parameter a
Der Parameter a gibt an, wie stark die Kurve in y-Richtung gestreckt ist.

Der Höhenunterschied bei der roten Wasserstandskurve ist doppelt so groß wie bei der einfachen Sinuskurve. Bei der einfachen Sinuskurve ist ja a=1. Damit ist bei der roten Kurve a=2.
a berechnen
Bestimme den Abstand zwischen den maximalen und den minimalen Werten der Kurve. Teile anschließend durch 2.
a=Max-Min2=6-22=2
Den Parameter a bestimmst du, indem du vom größten Funktionswert den kleinsten abziehst und das Ergebnis anschließend durch 2 teilst.
a=Max-Min2
Allgemeine Funktionsgleichung: f(x)=a⋅sin(b⋅(x-c))+d
Parameter d
Der Parameter d gibt an, wie stark die Kurve in y-Richtung verschoben ist.

Schau dir an, wie die Nullstellen der einfachen Sinuskurve verschoben sind. Die rote Kurve ist um 4 Einheiten nach oben verschoben.
d berechnen
Berechne den durchschnittlichen Wasserstand. Dazu addierst du den minimalen und den maximalen Wasserstand (die beiden Werte hast du gerade schon verwendet) und teilst das Ergebnis durch 2.
d=Max+Min2=6+22=4
Den Parameter d bestimmst du, indem du den größten Funktionswert und den kleinsten addierst und das Ergebnis anschließend durch 2 teilst.
d=Max+Min2
Allgemeine Funktionsgleichung: f(x)=a⋅sin(b⋅(x-c))+d

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Parameter b
Der Parameter b gibt an, wie stark die Kurve in x-Richtung gestaucht ist. Bestimme dazu die Periodenlänge.

b berechnen
Die Periode der einfachen Sinuskurve ist 2π. Die Periodenlänge der roten Kurve ist 12.
b berechnest du so:
b=2πPeriodenlaenge=2⋅π12=π6
Den Parameter b bestimmst du, indem du die Periodenlänge misst und anschließend 2π durch diesen Messwert teilst.
b=2πPeriodenlaenge
Allgemeine Funktionsgleichung: f(x)=a⋅sin(b⋅(x-c))+d
Wieso gilt b=2πPeriodenlaenge? Die Periodenlänge der einfachen Sinuskurve ist 2π. Wenn der Parameter b den Wert 2π hätte, wäre die Periodenlänge der gestauchten Kurve 1. Wie beim Dreisatz gehst du nun von dieser neuen Kurve mit Periodenlänge 1 aus und streckst sie im Beispiel um den Faktor 12.
Parameter c
Der Parameter c gibt an, wie stark die Kurve in x-Richtung verschoben ist.
Üblicherweise wird die Sinuskurve um ein Vielfaches einer Viertelperiodenlänge verschoben. Hier siehst Du die Beispiele:
| Kurven- verhalten bei x=0 | Schemaskizze | Verschiebung um |
| steigend | 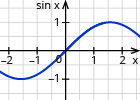 | 0 |
| maximal | 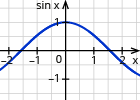 | 32π |
| fallend | 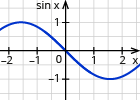 | π |
| minimal | 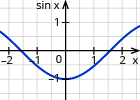 | π2 |

Es gibt mehrere Möglichkeiten, die Verschiebung zu bestimmen:
Erste Möglichkeit:
Du suchst den Punkt auf der Kurve, der sin(0) auf dem „Originalsinus“ entspricht. In unserer Kurve ist das z.B. -3 oder 9 (Sinus ist periodisch!). Das ist nun genau dein c, und Du erhältst mit c=-3
f(x)=2⋅sin(π6(x+3))+4.
Zweite Möglichkeit:
Bei der roten Kurve ist bei x = 0 gerade ein Maximum. Deshalb verschiebst Du die ganze Kurve um 3π2. Dafür musst Du nur das Argument bx verschieben und erhältst als neues Argument
f(x)=2⋅sin(π6x-32π)+4.
Allgemeine Funktionsgleichung: f(x)=a⋅sin(b⋅(x-c))+d
Ausflug mit dem Boot
Jetzt hast du die komplette Funktionsgleichung der roten Wasserstandskurve!
f(x)=2⋅sin(π6(x+3))+4.
Was kannst du nun damit anfangen?
Wasserstand für einen Zeitpunkt bestimmen
Kalles Segelboot hat einen Tiefgang von 3 m. Er möchte gerne wissen, ob er in 65 Stunden auslaufen kann.
Wenn du die Funktionsgleichung hast, kannst du z. B. mit dem Taschenrechner ausrechnen, wie hoch der Wasserstand zur entsprechenden Zeit ist. Dies wäre der Funktionswert für
x = 65.
f(65)≈2,27
Damit ist der Wasserstand nach 65 Stunden 2,3 m hoch und Kalle kann nicht auslaufen.
Andersrum: Wenn du den x-Wert berechnen möchtest, brauchst du meistens einen grafikfähigen Taschenrechner (GTR). Der kann dir auch eine Lösung der Gleichung ausgeben. Beim Sinus musst du mitunter mithilfe der Periodenlänge weitere Lösungen bestimmen.
Zeitpunkt bestimmen, wann ein vorgegebener Wasserstand erreicht wird
Kalle möchte seiner Nichte, die nicht von der Küste kommt, in zwei Tagen vorführen, wie es bei Ebbe aussieht. Er muss dafür wissen, wann das Wasser am niedrigsten steht. Dies wäre die Suche nach einem x-Wert, für den der Wasserstand f(x) = 2 m ist. Dies führt zu folgender Gleichung.
f(x)=2
2⋅sin(π6(x+3))+4=2
Die Lösungen lauten dann, da es zweimal Niedrigwasser gibt, dass Kalle entweder ca. zur Stunde 54 oder zur Stunde 66 mit seiner Nichte zum Deich gehen muss. Du suchst dabei diejenigen Lösungen, die zwischen 48 und 72 Stunden liegen, da dann der übernächste Tag ist (wenn du davon ausgehst, dass x = 0 um 0 Uhr ist).
 Bild: fotolia.com (philipus)
Bild: fotolia.com (philipus)

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen