Eigenschaften der Sinus- und Kosinusfunktion 2
Sinus und Kosinus „anpassen“
Du kennst nun die Sinus- und die Kosinusfunktion mit $$f(x)=sinx$$ und $$g(x)=cos x$$.
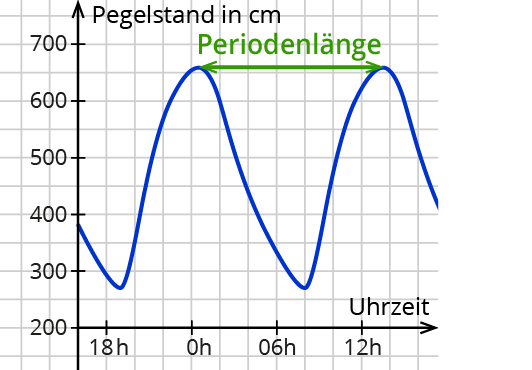
Wenn du „echte“ periodische Vorgänge aus der Realität mit der Sinus- oder Kosinusfunktion beschreiben willst, wird der Graph nicht so gut passen. Du müsstest zum Beispiel Periode oder Amplitude verändern können.
Das geht mit Parametern.

Sinus und Kosinus stauchen und strecken
Was passiert, wenn du alle Funktionswerte der Sinusfunktion mit einer Zahl multiplizierst?
Mathematisch: Nimm die Funktion $$f(x)=a*sin(x)$$ und setze unterschiedliche Werte für $$a$$ ein. Das sieht dann so aus:

- Der Parameter $$a$$ staucht oder streckt die Kurve in y-Richtung.
- Wenn $$a$$ zwischen $$-1$$ und $$+1$$ liegt, ist die Sinusfunktion gestaucht.
- Wenn $$a$$ größer als $$1$$ oder kleiner als $$-1$$ ist, ist die Sinusfunktion gestreckt.
- Wenn $$a$$ kleiner als 0 ist, wird die Sinusfunktion an der x-Achse gespiegelt.
- Der Parameter $$a$$ verändert die Amplitude der Funktion. Die Amplitude ist so groß wie a. (Aber mit positivem Vorzeichen $$+$$.)
Für $$g(x)=acos x$$ funktioniert die Stauchung oder Streckung ganz genauso.
Stauchen und Strecken in x-Richtung
Du kannst auch probieren, was passiert, wenn du die x-Werte erst mit einer Zahl multiplizierst und dann den Sinus bildest.
Die Funktion heißt dann $$f(x)=sin(b*x)$$. So sieht die Funktion für verschiedene $$b$$ aus:

- Der Parameter $$b$$ staucht oder streckt die Sinusfunktion in x-Richtung.
- Wenn $$b$$ zwischen $$-1$$ und $$+1$$ liegt, ist die Sinusfunktion gestreckt.
- Wenn $$b$$ größer als $$1$$ oder kleiner als $$-1$$ ist, wird die Funktion gestaucht.
- Wenn $$b$$ kleiner als $$0$$ ist, wird die Sinusfunktion an der y-Achse gespiegelt.
- Der Parameter $$b$$ verändert die Periodenlänge. $$b$$ gibt an, wie viel mal schneller die Schwankung stattfindet.
Für $$g(x)=cos(b*x)$$ funktioniert die Stauchung oder Streckung ganz genauso.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Kombiniert
Kannst du eine Funktion mit a und b bauen? Klar.:-)
Beispiel:
Eine Kurve soll um 4 m um einen Mittelwert schwanken und dreimal so schnell ablaufen wie die normale Sinusschwankung. Dann heißt die Funktionsgleichung $$f(x)=4*sin(3x)$$.
$$a=4$$ bewirkt, dass die Sinusfunktion zwischen $$-4$$ und $$4$$ schwankt.
$$b=3$$ bewirkt, dass die Schwankung dreimal so schnell abläuft. Wo die ursprüngliche schwarze Kurve einen Berg hat, schwankt die gestauchte blaue Kurve nun dreimal.

Wenn du beide Parameter gleichzeitig in die Gleichung schreibst, lautet sie $$f(x)=a*sin(b*x)$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen