Höhensatz und Kathetensatz

Es gibt noch 2 weitere Berechnungen, die sich auf rechtwinklige Dreiecke beziehen. Sie leiten sich aus dem Satz des Pythagoras ab.

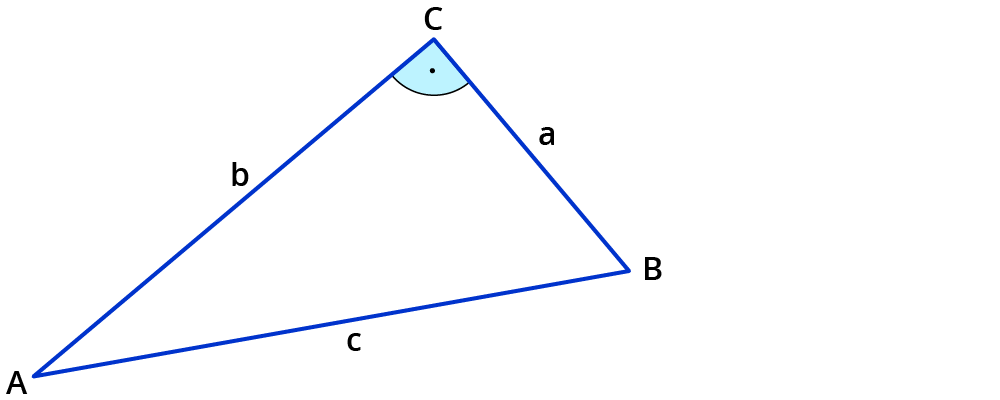
Dazu zeichnest du die Höhe auf der Hypotenuse des Dreiecks ein. Die Hypotenuse (die längste Seite im Dreieck) wird durch die Höhe auf ihr in 2 Teile geteilt.

Meistens heißen die Teilstücke $$q$$ und $$p$$.

Die neuen beiden Sätze, die du jetzt lernst, sind der Höhensatz und der Kathetensatz.

Der Höhensatz

Der Höhensatz lautet:

$$h^2=q*p$$

In Worten gesprochen bedeutet der Höhensatz: Zeichnest du ein Quadrat mit der Seitenlänge $$h$$, ist das genauso groß wie der Flächeninhalt des Rechtecks mit den Seiten $$p$$ und $$q$$.

Beispiel:
$$h=4$$ $$cm$$
$$q=8$$ $$cm$$
$$p=2$$ $$cm$$

Hier ist das Quadrat mit der Seitenlänge $$h =4$$ $$cm$$ eingezeichnet. Der Flächeninhalt ist hier $$16$$ $$cm^2$$. Du rechnest $$4*4 = 16$$ $$cm^2$$.

Jetzt ist auch das Rechteck $$q*p$$ eingezeichnet. Den Flächeninhalt berechnest du mit $$2*8=16$$ $$cm^2$$.

Das ist ein Beispiel für den Höhensatz. Das geht mit jedem rechtwinkligen Dreieck. Allgemein gilt $$h^2=q*p$$.

Der Kathetensatz

Den Kathetensatz gibt es für beide Katheten $$a$$ und $$b$$:

$$a^2 = c*p$$
$$b^2 = c*q$$

Erklärt wird dir hier das Beispiel mit $$b^2$$.

In Worten gesprochen bedeutet der Kathetensatz: Das Quadrat mit der Seitenlänge $$b$$ ist flächengleich zu dem Rechteck mit den Seitenlängen $$c$$ und $$q$$.

Beispiel:

$$b^2 stackrel(?)= c*q$$

$$5^2=6,25*4$$ (Zahlen einsetzen)

$$25=25$$

Das passt!

Im Bild sieht das so aus:

Beweis des Höhensatzes

Den Höhensatz kannst du mit dem Satz des Pythagoras beweisen.

Das Dreieck wird durch die Höhe in 2 rechtwinklige Dreiecke geteilt. In beiden Dreiecken kannst du den Satz des Pythagoras anwenden.

$$h_c^2+p^2=a^2$$

$$h_c^2+q^2=b^2$$

Außerdem gilt der Satz des Pythagoras in dem großen Dreieck:

$$a^2$$ $$+$$ $$b^2$$ $$=c^2$$

Beide Pythagorasgleichungen der kleinen Dreiecke setzt du in die Gleichung für das große Dreieck ein.

$$a^2$$ $$+$$ $$b^2$$ $$=c^2$$

$$h_c^2+p^2$$ $$+$$ $$h_c^2+q^2$$ $$=c^2$$ $$|$$zusammenfassen

$$2h_c^2+p^2+q^2=c^2$$ $$|$$setze $$(p+q)$$ für $$c$$ ein

$$2h_c^2+p^2+q^2=(p+q)^2$$ $$|$$Binomische Formel anwenden

$$2h_c^2+p^2+q^2=p^2+2pq+q^2$$ $$|$$$$-p^2$$ und $$-q^2$$

$$2h_c^2=2pq$$ $$|:2$$

$$h_c^2=p*q$$

Die letzte Zeile ist der Höhensatz! Du hast mithilfe von Umformungen den Höhensatz erhalten. Damit ist er bewiesen.

Beweis des Kathetensatzes

Im Beweis des Kathetensatzes wird der Höhensatz benutzt. Das darfst du tun, weil du den Höhensatz ja gerade bewiesen hast.

Es geht bei diesem Beweis darum, dass durch Umstellung des Satzes des Pythagoras der Kathetensatz $$a^2 = p * c$$ entsteht.

Das blaue Dreieck wird für den Pythagoras verwendet.

$$a^2=p^2+h_c^2$$ $$|$$ Höhensatz anwenden: $$h_c^2=p*q$$

$$a^2=p^2+p*q$$ $$|$$$$p$$ ausklammern

$$a^2=p*(p+q)$$ $$|$$$$p+q$$ ist gleich $$c$$

$$a^2=p*c$$

Das war zu beweisen. Für die andere Kathete $$b$$ würdest du das andere Dreieck mit der Seite $$q$$ nehmen.