Oberflächeninhalt der Kugel berechnen
Die Erde ist eine Kugel
Viele Gegenstände sind kugelförmig. Oder fast kugelförmig: Den Planeten Erde kannst du durch eine Kugel annähern, obwohl er an Nord- und Südpol „platter“ ist.
Bild: iStockphoto.com (evirgen)
Wie groß ist die Erdoberfläche?
Um die Oberfläche zu berechnen, brauchst du ein paar Eigenschaften der Kugel.
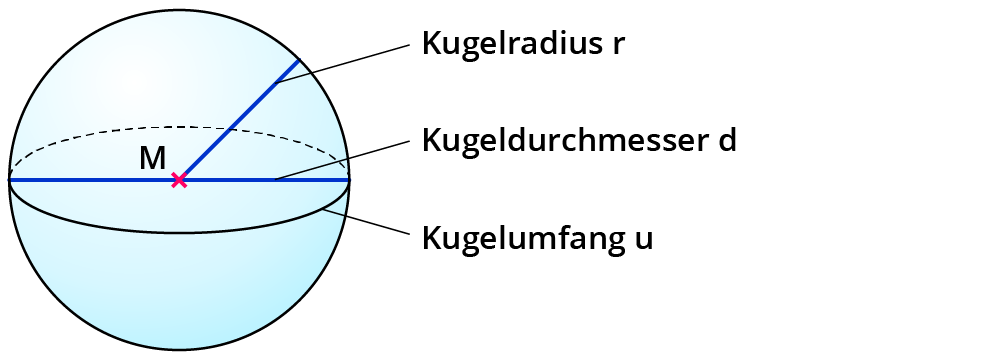
Die Kugel hat einen Mittelpunkt. Alle Punkte der Oberfläche sind vom Mittelpunkt gleich weit entfernt. Der Abstand ist der Radius oder Kugelradius.
Eine Kugel ist ein geometrischer Körper, den du erhältst, wenn du einen Kreis um seinen Durchmesser rotieren lässt.
Was ist die Oberfläche einer Kugel?
Die Oberfläche einer Kugel besteht aus einer gekrümmten Fläche. Am besten kannst du sie dir vorstellen, wenn du die Kugel aufschneiden würdest. Stell dir vor, du schneidest die Kugeloberfläche in viele Streifen.
So berechnest du den Oberflächeninhalt einer Kugel: $$O=pi*4*r^2$$ oder $$O=pi*d^2$$
- $$r$$ Radius
- $$d$$ Durchmesser
- $$pi$$ Kreiszahl
Die Oberfläche ist die Fläche, die du berühren kannst, wenn du die Kugel in der Hand hältst.
$$O = pi *4 * r^2 = pi * d^2$$ , denn $$2 * r = d$$ und somit $$(2 * r)^2 = 4 * r^2 = d^2$$
Oberfläche einer Kugel berechnen
Gegeben ist eine Kugel mit $$d =$$ $$8$$ $$cm$$.
Du weißt:
$$d = 2 * r$$
$$d/2 = r$$
$$(8 cm)/2 = r$$
$$4 cm = r$$
Um die Oberfläche der Kugel zu berechnen, gehst du so vor:
$$O=pi*4*r^2$$
$$O=pi*4*(4 cm)^2$$
$$O=pi*4*16 cm^2$$
$$O = 201,06 cm^2$$
Oder:
$$O = pi * d^2$$
$$O = pi * (8 cm)^2$$
$$O = pi *64 cm^2$$
$$O = 201,06 cm^2$$
Nutze die $$pi$$ -Taste auf deinem Taschenrechner.
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Den Radius bei einer gegebenen Oberfläche berechnen
Gegeben ist eine Kugel mit Oberfläche $$O = 453,54 cm^2$$.
Um den Radius der Kugel zu berechnen, gehe so vor:
1. Setze die gegebene Oberfläche in die Formel ein:
$$O=pi*4*r^2$$
$$453,54 cm^2$$$$=pi*4*r^2$$
2.. Löse die Formel nach $$r$$ auf:
$$453,54 cm^2$$$$=pi*4*r^2$$ |$$:4$$ |$$:pi$$
$$(453,54 cm^2)/(pi*4)$$$$=r^2$$ |$$sqrt$$
$$sqrt((453,54 cm^2)/(pi*4))$$$$=r$$
$$sqrt(36,09 cm^2)=r$$
$$6,01 cm = r$$
Du kannst auch erst die Formel nach $$r$$ auflösen und dann die gegebene Oberfläche einsetzen:
$$O=pi*4*r^2$$ |$$:4$$ |$$:pi$$
$$O /(pi*4)=r^2$$ |$$sqrt$$
$$sqrt(O /(pi*4))=r$$
$$sqrt((453,54 cm^2)/(pi*4))$$$$=r$$
$$sqrt(36,09 cm^2)=r$$
$$6,01 cm = r$$
Den Durchmesser bei einer gegebenen Oberfläche berechnen
Gegeben ist eine Kugel mit einer Oberfläche von $$O = 453,54$$ $$cm^2$$.
Um den Durchmesser der Kugel zu berechnen, gehe so vor:
1. Setze die gegebene Oberfläche in die Formel ein:
$$O=pi*d^2$$
$$453,54 cm^2$$$$=pi*d^2$$
2. Löse die Formel nach $$d$$ auf:
$$453,54 cm^2$$$$=pi*d^2$$ |$$:pi$$
$$(453,54 cm^2)/pi=d^2$$ |$$sqrt$$
$$sqrt((453,54 cm^2)/pi)=d$$
$$sqrt(144,37 cm^2)=d$$
$$12,02 cm=d$$
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
