Eigenschaften der Pyramide untersuchen
Arten von Pyramiden
Faszinieren dich auch die Pyramiden aus dem alten Ägypten?

Bild: fotolia.com
In Pyramiden steckt jede Menge Mathematik. Es gibt verschiedene Arten von Pyramiden:

Die Grundfläche (blau gefärbt) einer Pyramide gibt ihr den Namen.
Pyramiden sind spitz zulaufende Körper, die eine eckige, namengebende Grundfläche besitzen.
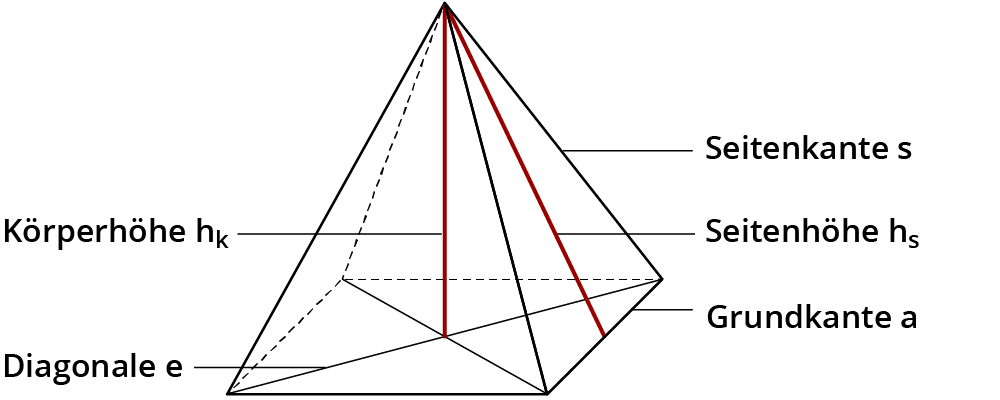
Pyramide - Begriffe und Eigenschaften
Zum Berechnen von Pyramiden benötigst du einige Begriffe, die du hier kennen lernst.

| Grundseite | a |
| Seitenkante | s |
| Seitenhöhe | hs |
| Körperhöhe | hk |
| Diagonale | e, f |
| Grundfläche | G |
| Seitenfläche | A |
Vom Netz zur Oberfläche
Wie ein Netz entsteht und wie die Oberfläche einer quadratischen Pyramide berechnet wird, siehst du hier.
Pyramide (allgemein): O = Grundfläche + Mantel
Quadratische Pyramide: O = a² + 2 a hs

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
So berechnest du eine quadratische Pyramide.
Beispiel

gegeben:
a=5 cm
hs =8 cm
Rechnung:
O= Grundfläche + Mantel
O= a2 + 2⋅a⋅hs
O= 52 +2⋅5⋅8
O=105 cm2
Berechnung der Seitenhöhe hs einer quadratischen Pyramide.

gegeben: O=504 mm2
a=12 mm
Rechnung:
1. Den Mantel der Pyramide bestimmen.
Die Grundfläche (G=a2=122=144 mm2) kannst du von der Oberfläche abziehen und rechnest dann nur noch mit dem Mantel.
M=O –G=504–144=360 mm2
2. Die Mantelformel nun nach hs umstellen.
M=2·a·hs ∣:(2·a)
M2·a=hs
3. Jetzt die Werte in die Formel einsetzen und du hast die Seitenhöhe berechnet.
hs=M2·a=3602·12=15 mm
Oberfläche einer quadratischen Pyramide. Rechnen mit a und hk.
Manchmal sind andere Werte der Pyramide gegeben und du musst die notwendigen Größen erst ermitteln (meist mit Pythagoras).

Beispiel:
gegeben: a=5 cm
hk =8 cm
Rechnung:
1. hs mit Pythagoras berechnen (Hypotenuse gesucht):
hs=√h2k+(a2)2
hs=√82+(52)2
hs ≈ 8,38 cm
2. O berechnen:
O= Grundfläche + Mantel
O=a2+2⋅a⋅hs
O=52+2⋅5⋅8,38
O ≈ 108,80 cm2

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Oberfläche einer quadratischen Pyramide. Rechnen mit a und s.

Beispiel
gegeben: a=25 cm
s=18 cm
Rechnung:
hs ist eine Kathete des rechtwinkligen Dreiecks „Seitenkante – halbe Grundseite – Seitenhöhe“. Der rechte Winkel liegt zwischen der Seitenhöhe und der halben Grundseite.
1. hs gesucht
hs=√s2-(a2)2
hs=√182-(252)2
hs ≈ 12,95 cm
2. O berechnen:
O= Grundfläche + Mantel
O =a2+2⋅a⋅hs
O=252+2⋅25⋅12,95
O ≈ 1272,50 cm2
Oberfläche einer quadratischen Pyramide. Rechnen mit s und hk
Dieses Mal ist keiner der zwei notwendigen Werte gegeben. Beide müssen erst (mit Pythagoras) ermittelt werden.

Beispiel:
gegeben: s=18 cm
hk =12 cm
Rechnung:
1. e2 berechnen
Du rechnest mit dem Dreieck „Seitenkante – Körperhöhe – halbe Diagonale“. Der rechte Winkel liegt zwischen Körperhöhe und halber Diagonale. Du suchst eine Kathete.
e2=√s2-(hk)2
e2=√182-122
e2 ≈ 13,42 cm
Daraus ergibt sich: e=2⋅e2=2⋅13,42 ≈ 26,84 cm
2. a berechnen:
Die Diagonale eines Quadrats wird mit der Formel e=a·√2 berechnet. Durch Umstellung erhältst du:
a=e√2
a=26,84√2
a ≈ 18,98 cm
3. hs berechnen:
hs=√h2k+(a2)2
hs=√122+(18,982)2
hs ≈ 15,30 cm
4. O berechnen:
O=a2+2⋅a⋅hs=18,982+2⋅18,98⋅15,30≈ 941,03 cm2
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen