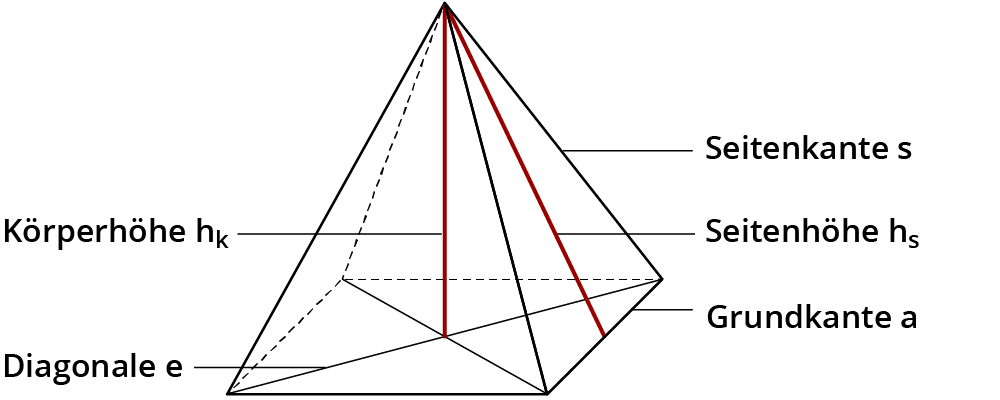
Oberflächeninhalt der Pyramide berechnen
Verschiedene Pyramiden
Hier siehst du Bilder nicht quadratischer Pyramiden, die alle ein regelmäßiges Vieleck als Grundfläche haben.
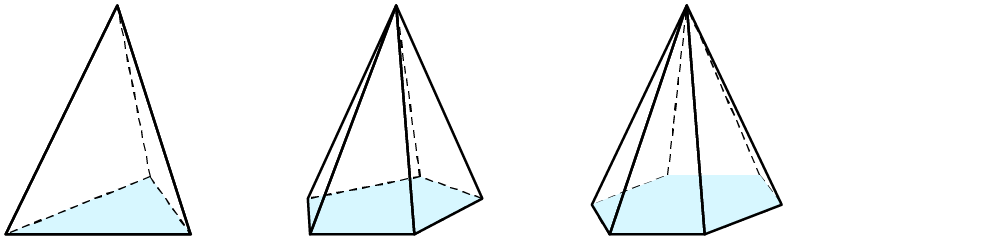
Diese Pyramiden berechnest du so:
- Die Grundfläche wird entsprechend ihrer Form berechnet.
- Ermittle die Anzahl der Dreiecksflächen, die für den Mantel nötigt sind. (Dreieckige Pyramide $$rArr$$ 3 Dreiecksflächen, Fünfeckige Pyramide $$rArr$$ 5 Dreiecksflächen, usw.)
- Berechne anschließend (möglichst günstig) die Mantelfläche.
Falls die Höhe nicht zentriert auf der Mitte steht, besteht der Mantel aus unterschiedlichen Dreiecken, die du einzeln berechnest.
Auf den nächsten Seiten wirst du Berechnungen für einige Pyramidenarten kennen lernen.
Rechteckige Pyramiden
So rechnest du mit rechteckigen Pyramiden:
Meistens nutzt du diese Beschriftung:
| Grundseite | $$a, b$$ |
| Seitenkante | $$s$$ |
| Seitenhöhe | $$h_a, h_b$$ |
| Körperhöhe | $$h_k$$ |
| Diagonale | $$e$$ oder $$f$$ |
| Grundfläche | $$G$$ |
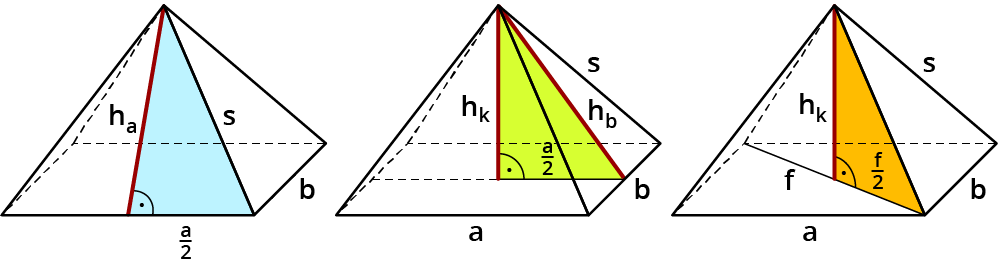
Berechnung einer rechteckigen Pyramide

gegeben:
$$a = 7$$ $$cm$$
$$h_a = 10,6$$ $$cm$$
$$b = 5$$ $$cm$$
$$h_b = 10,3$$ $$cm$$
Berechne die Oberfläche der Pyramide.
Lösung:
Die Grundfläche ist ein Rechteck. Die 2 gegenüberliegenden Seitenflächen sind gleich. Also berechnest du 2 unterschiedliche Dreiecksflächen, die du anschließend addierst.
Grundfläche: Ein Rechteck berechnest du mit $$a*b$$.
Mantel:
- Die Dreiecksfläche mit der Grundseite $$a$$ (Formel: $$(a*h_a)/2$$) ist zweimal vorhanden. Multipliziere sie also mit 2 und du erhältst als Formel $$a*h_a$$.
- Genauso berechnest du die Dreiecksfläche mit der Grundseite $$b$$. Rechne $$b*h_b$$.
- Du berechnest den Mantel, indem du die beiden Werte addierst.
Gesamte Oberfläche: O $$=$$ Grundfläche $$+$$ Mantelfläche
Grundfläche
$$uarr$$
$$O=$$ $$a*b$$ $$ + $$ $$a*h_a$$ $$+$$ $$b*h_b$$ $$=7*5+7*10,6+5*10,3=160,7$$ cm³
$$darr$$ $$darr$$
2 Dreiecke mit der 2 Dreiecke mit der
Grundseite a Grundseite b
Oberfläche $$=$$ Grundfläche $$+$$ Mantelfläche $$=a*b+a*h_a+b*h_b$$
Berechnung mit der Körperhöhe $$h_k$$

Gegeben:
$$a = 7$$ $$cm$$
$$b = 5$$ $$cm$$
$$h_k = 12$$ $$cm$$
Berechne die Oberfläche der rechteckigen Pyramide.
Lösung:
1. $$h_a$$ berechnen
$$b/2$$, $$h_k$$ und $$h_a$$ bilden ein rechtwinkliges Dreieck. Zwischen $$b/2$$ und $$h_k$$ liegt der rechte Winkel. Es fehlt für die Berechnung mit Pythagoras die Hypotenuse.
$$h_a = sqrt((b/2)^2+h_k^2 ) = sqrt((5/2)^2+12^2) approx 12,26$$ $$cm$$
2. $$h_b$$ berechnen (wie $$h_a$$ nur mit anderen Werten)
$$h_b= sqrt((a/2)^2+h_k^2) = sqrt((7/2)^2+12^2 ) = 12,50$$ $$cm$$
3. Gesamtfläche berechnen
$$O =$$ $$A_(Grundfläche)$$ $$+$$ $$Mantel $$
$$=$$ $$a*b$$ $$+$$ $$a*h_a + b*h_b $$
$$=$$ $$7*5$$ $$+$$ $$7*12,26 + 5*12,5$$
$$approx 183,32$$ $$cm^2$$
Dreieckige Pyramiden
Für Berechnungen mit dreieckigen Pyramiden gilt:
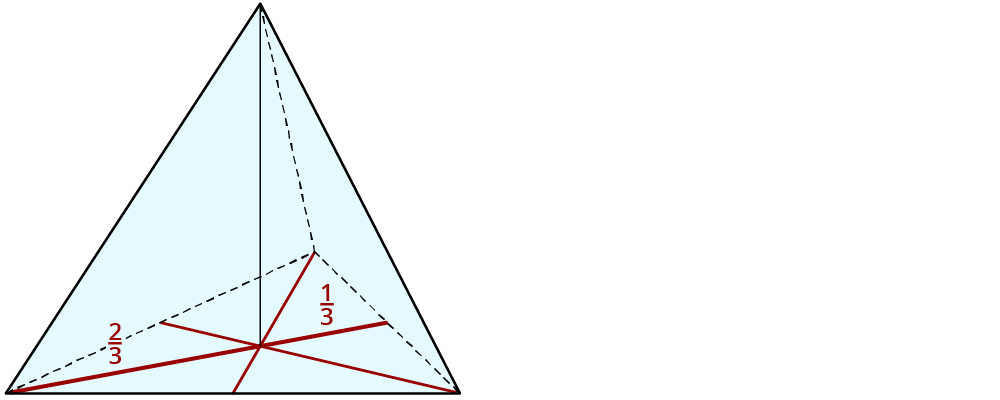
Die Seitenhalbierenden eines Dreiecks treffen sich im Schwerpunkt.
Der Schwerpunkt teilt jede Seitenhalbierende im Verhältnis
$$1/3$$ (Entfernung von der Grundseite) zu
$$2/3$$ (Entfernung von der Dreiecksspitze).
Berechnung eines Tetraeders
Ein Tetraeder ist eine besondere Pyramide: Alle Flächen sind gleichseitige, gleich große Dreiecke.
$$h_a = 9$$ $$cm$$
Berechne die Oberfläche des Tetraeders.
Lösung:
Bei einem gleichseitigen Dreieck sind Seitenhalbierende und Seitenhöhe $$h_a$$ gleich.
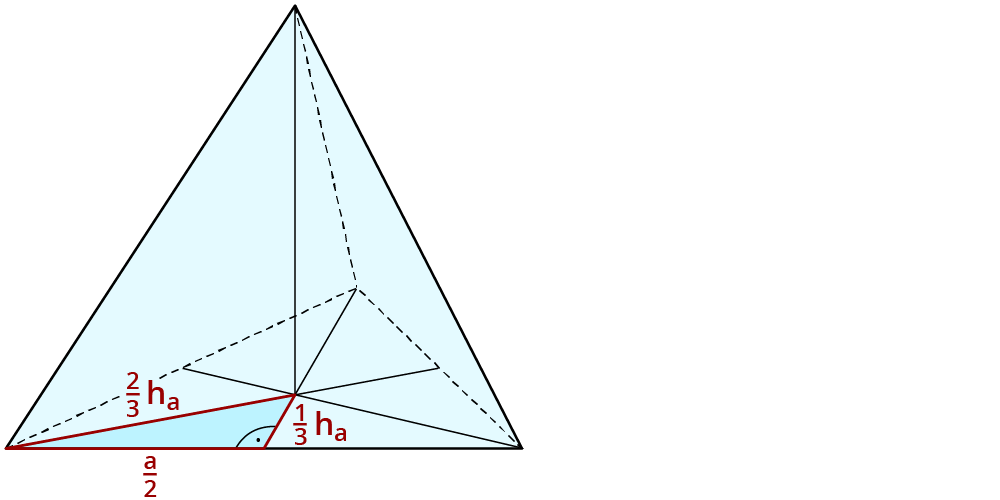
$$a$$ berechnen
$$a/2$$ ist im Dreieck $$1/3 h_a$$ und $$2/3 h_a$$ eine Kathete.
$$a/2= sqrt((2/3 h_a )^2- (1/3 h_a )^2 ) =sqrt((2/3 *9 )^2- (1/3*9)^2 )$$
$$a/2 approx 5,196$$ $$cm$$
$$ rArr a approx 10,39$$ $$cm$$Oberfläche $$O$$ berechnen
$$O=4*$$ Grundfläche, da die Grundfläche genauso groß ist wie die Seitenflächen
$$O=4* (a* h_a)/2=2*a* h_a=2*10,39*9=187,02$$ $$cm^2$$
Sechseckige Pyramiden
Berechne die Oberfläche dieser regelmäßigen sechseckigen Pyramide. $$a = 5$$ $$dm$$ $$h_a = 10$$ $$dm$$
Lösung:
Die Grundfläche besteht aus sechs gleichseitigen Dreiecken, die die Seitenlänge a haben.
- $$h_g$$ (Höhe der Grundflächendreiecke) berechnen
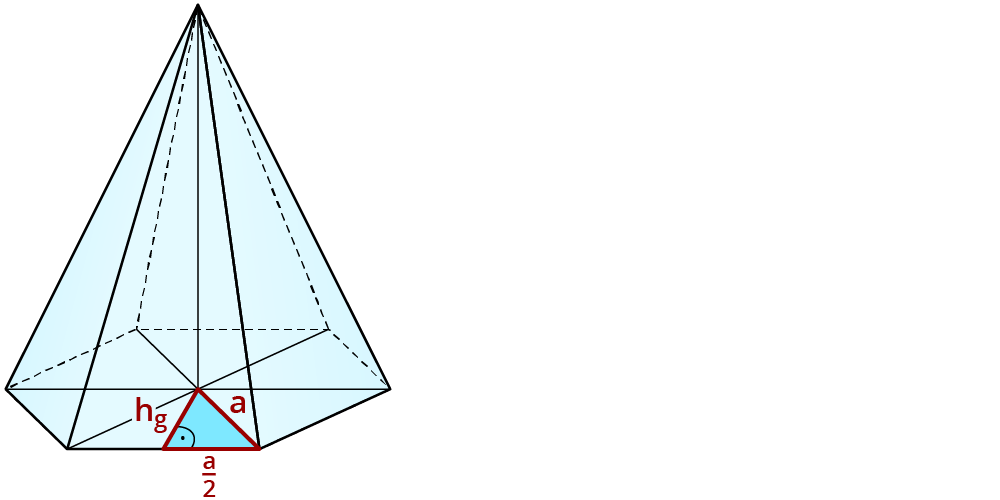
$$h_g= sqrt(a^2- (a/2 )^2 ) = sqrt(5^2- (5/2)^2 ) approx 4,33$$ $$dm^2$$ - Die Grundfläche $$G$$ setzt sich aus 6 Einzeldreiecken zusammen, daher 6-mal die Dreiecksformel.
$$G = 6* (a* h_g)/2= 3*a* h_g) = 3*5* 4,33 approx 64,95$$ $$dm^2$$
Der Mantel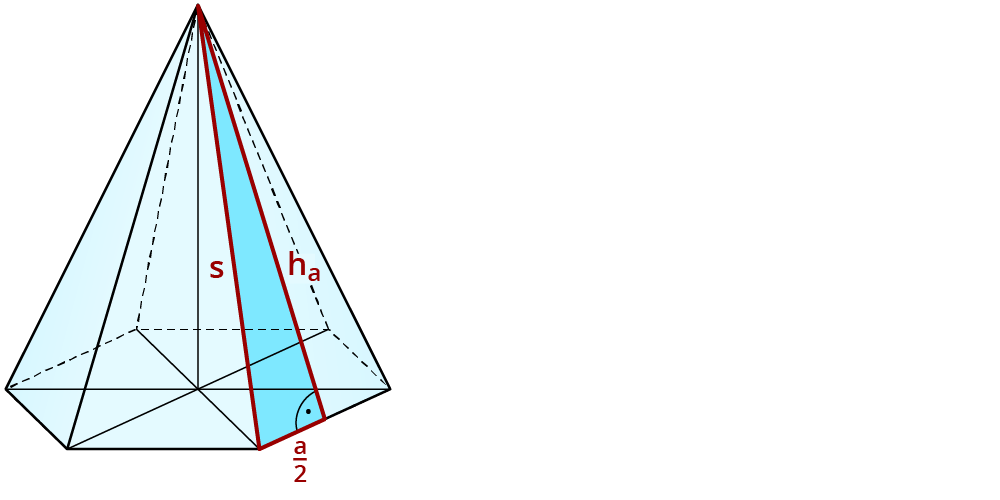
Auch der Mantel setzt sich ebenfalls aus 6 gleichen Dreiecken zusammen. $$M = 6* (a * h_a)/2=3*a*h_a=3*5*10=150$$ $$dm^2$$
Die Oberfläche
$$O=G+M=64,95+150 approx 214,95$$ $$dm^2$$
Formel für sechseckige regelmäßige Pyramidenoberflächen
Falls du eine sechseckige, regelmäßige Pyramide lieber mit einer Formel berechnen willst, siehst du hier, wie diese entsteht.
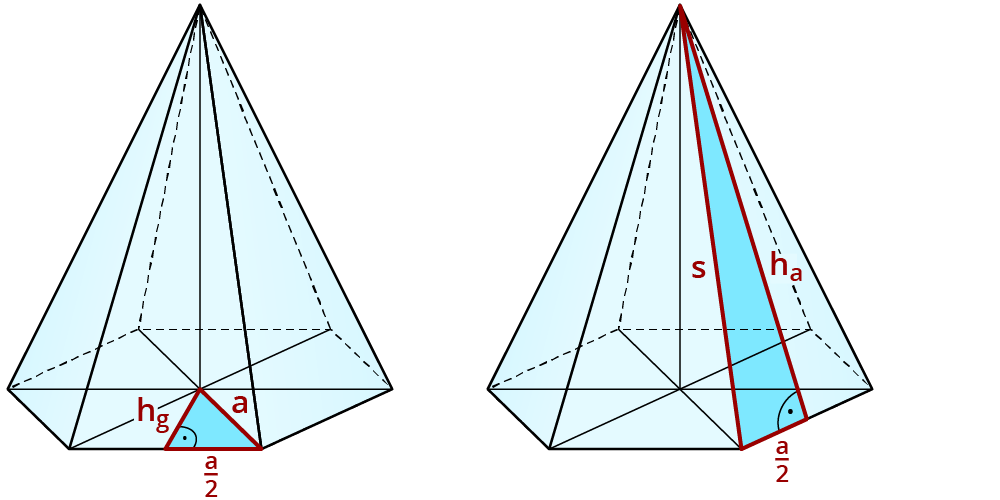
Die Formel für die Höhe $$h_g$$ wird so umgestellt.
$$(h_g)^2= a^2- (a/2 )^2 = a^2- a^2/4 = 3/4 a^2$$
Also:
$$(h_g)^2=3/4 a^2$$ $$ | sqrt$$
$$h_g= 1/2 a sqrt3$$
Die Grundfläche G setzt sich aus 6 Einzeldreiecken zusammen, daher 6-mal die Dreiecksformel. Die Höhenformel wird entsprechend eingesetzt und du erhältst die Grundflächenformel:
$$G= 6* (a * h_g)/2=6* (a* 1/2 a sqrt3)/2= 3*a*1/2 a sqrt3=$$ $$ 1,5 a^2 sqrt3$$
In die Oberflächenformel wird die Grundfläche mit eingebaut.
$$O=1,5 a^2 sqrt3+6*(a* h_a)/2=$$ $$ 1,5 a^2 sqrt3+3*a*h_a$$
Berechnung für $$a = 5$$ $$dm$$ $$h_a = 10$$ $$dm$$:
$$O=1,5 a^2 sqrt3+3*a*h_a=1,5*5^2*sqrt3+3*5*10 approx 214,95$$ $$dm^2$$
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen