Jetzt wird’s praktisch!

Jetzt bist du fit für Anwendungsaufgaben!

Bei Anwendungsaufgaben sind oft Bilder mit dabei, die das Problem erklären. Manchmal musst du erst selbst eine Skizze anfertigen, um die Aufgabe zu verstehen.

Neuer Schritt für Anwendungsaufgaben

0) Als erstes musst du die Aufgabe verstehen. Du trägst die gegebenen Werte in eine Skizze ein oder du markierst das Gegebene farbig.

Das weitere Vorgehen ist dir bekannt.

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
2) Stelle die Verhältnisgleichung auf.
3) Rechne die gesuchte Strecke aus.

4) Schreibe einen Antwortsatz.

Beispiel 1

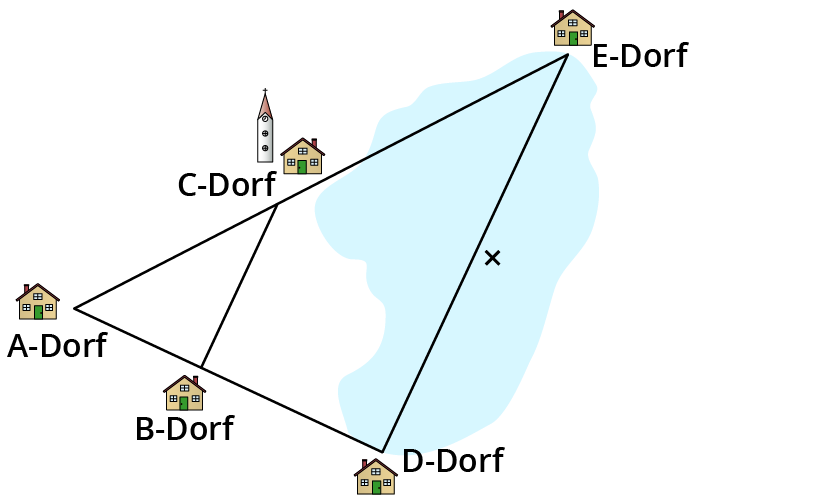
Du sollst berechnen, wie weit D-Dorf und E-Dorf voneinander entfernt sind. Da dort ein See liegt, kann niemand die Strecke einfach abfahren. Die Entfernungen der anderen Orte sind aber zum Teil bekannt. A-Dorf ist 7 km von B-Dorf entfernt. A-Dorf ist 17 km von D-Dorf entfernt. B-Dorf und C-Dorf liegen 9 km auseinander.

0) Skizze

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
Du nimmst den 2. Strahlensatz, denn die parallelen Strecken sind wichtig.

2) Stelle die Verhältnisgleichung auf.
$$x/9=17/7$$

3) Rechne die gesuchte Strecke aus.
$$x/9=17/7$$ $$|*9$$

$$x=(17*9)/7 approx 21,857$$ $$km$$

4) Schreibe einen Antwortsatz.
D-Dorf und E-Dorf sind rund $$21,857$$ $$km$$ auseinander.

Beispiel 2

Jana will die Höhe des Maibaums bestimmen. Sie kann seinen Schatten messen. Er ist 8 m lang. Sie selbst ist 1,60 m groß und stellt sich so, dass ihr Schatten genau mit dem Schattenende zusammenfällt. Jana selbst steht 6 m vom Maibaum entfernt. Wie hoch ist der Maibaum?

0) Skizze

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
Nimm den 2. Strahlensatz, denn die parallelen Strecken sind wichtig.

2) Stelle die Verhältnisgleichung auf.
$$x/8=(1,60)/2$$

3) Rechne die gesuchte Strecke aus.

$$x/8=(1,60)/2$$ $$|*8$$

$$x=(1,6*8)/2=6,4$$ $$m$$

4) Schreibe einen Antwortsatz.
Der Maibaum ist $$6,4$$ $$m$$ hoch.

Aufgabe mit sich schneidenden Geraden

Es gibt Anwendungsaufgaben mit sich schneidenden Geraden. Hier ist der Abstand der Orte $$B$$ und $$A$$ gesucht. Der Ort $$B$$ liegt auf dem Schnittpunkt zweier Geraden. $$bar(DE)$$ und $$bar(AF)$$ sollen parallel sein.

0) Skizze

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
Du nimmst den 1. Strahlensatz, denn die parallelen Strecken sind unwichtig.

2) Stelle die Verhältnisgleichung auf.
$$x/160=560/240$$

3) Rechne die gesuchte Strecke aus.
$$x/160=560/240$$ $$|*160$$

$$x=(560*160)/240$$

$$x=373,bar 3 = 373 1/3$$

4) Schreibe einen Antwortsatz.
Die Strecke ist gerundet $$373,33$$ $$m$$ lang.

Aufgaben mit Kameras

Du kannst Aufgaben mit Kameras mithilfe des Strahlensatzes lösen.

Hier ist allerdings eine Uminterpretation der Strahlensatzsituation nötig.

Beispiel:

Du bist 3 m von einer Kerze entfernt. Du fotografierst die mit einer 3 cm breiten Kamera. Auf dem Bild ist die Kerze 0,5 cm hoch. Wie hoch war sie in echt?

0) Skizze
Skizze 1:

Skizze 2 mit Uminterpretation:

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
Hier erkennst du den 2. Strahlensatz an sich schneidenden Geraden.

2) Stelle die Verhältnisgleichung auf.
$$x/(0,5)=300/3$$

3) Rechne die gesuchte Strecke aus.
$$x/(0,5)=300/3$$ $$|*0,5$$

$$x=(300*0,5)/3=50$$ $$cm$$

4) Schreibe einen Antwortsatz.
Die Kerze war in echt einen halben Meter hoch.

Um die Ecke gedacht

Jetzt bist du fit für komplexe Aufgaben, die verschiedene Mathethemen kombinieren.

Manche Geometrieaufgaben haben auf den ersten Blick gar nichts mit dem Strahlensatz zu tun. Dann musst du erst die Strahlensatzfiguren suchen, die dir weiterhelfen.

Aufgabe:

In einem gleichschenkligen Trapez mit $$a = 20$$ $$cm$$, $$b = 12$$ $$cm$$ und $$c = 5,6$$ $$cm$$ sollst du herausfinden, wie groß der gefärbte Anteil am gesamten Trapez ist.

Zuerst berechnest du die Höhe im Trapez mithilfe des Satzes von Pythagoras:

$$rArr h^2=12^2-7,2^2$$

$$h^2=144-51,84$$

$$= 92,16$$ $$|sqrt( )$$

$$h=9,6$$ $$cm$$

Jetzt wird die Gesamtfläche berechnet:

$$A=(a+c)/2 *h = (20+5,6)/2 *9,6$$

$$=122,88$$ $$cm^2$$

Jetzt kannst du auch die Fläche des grünen Dreiecks berechnen.

$$A_(△) = (20*9,6)/2=96$$ $$cm^2$$

Um die Ecke gedacht

Erst jetzt kommt der Strahlensatz zum Einsatz. Dir fehlt die Höhe des weißen Dreiecks zur Flächenberechnung.

Du wendest den 1. Strahlensatz an, um erst mal die Strecke $$x$$ zu bekommen.

$$x/(9,6)=(7,2)/(12,8)$$ $$|*9,6$$

$$x=5,4$$ $$cm$$

Berechne nun das dunkelblaue Teilstück:

$$9,6-5,4=4,2$$ $$cm$$

Wieder mit dem 1. Strahlensatz stellst du eine Verhältnisgleichung auf, um die Höhe des weißen Dreiecks zu berechnen.

$$z/(4,2)=(2,8)/(5,6)$$ $$|*4,2$$

$$z=2,1$$ $$cm$$

Jetzt rechnest du den Flächeninhalt des weißen Dreiecks aus.

$$A_(△)=(g*h)/2$$

$$=(5,6*2,1)/2$$

$$=5,88$$ $$cm^2$$

Rechne nun die Flächeninhalte des grünen und weißen Dreiecks zusammen.

$$96+5,88=101,88$$ $$cm^2$$

Rote Fläche: $$text(Gesamtfläche)-101,88=122,88-101,88 = 21$$ $$cm^2$$

Jetzt kannst du den Anteil angeben:

$$21/(122,8) approx 0,17$$

Das sind ungefähr $$17%$$.