Beide Strahlensätze zusammen

Den 1. und den 2. Strahlensatz nutzt du, um eine unbekannte Strecke auszurechnen.

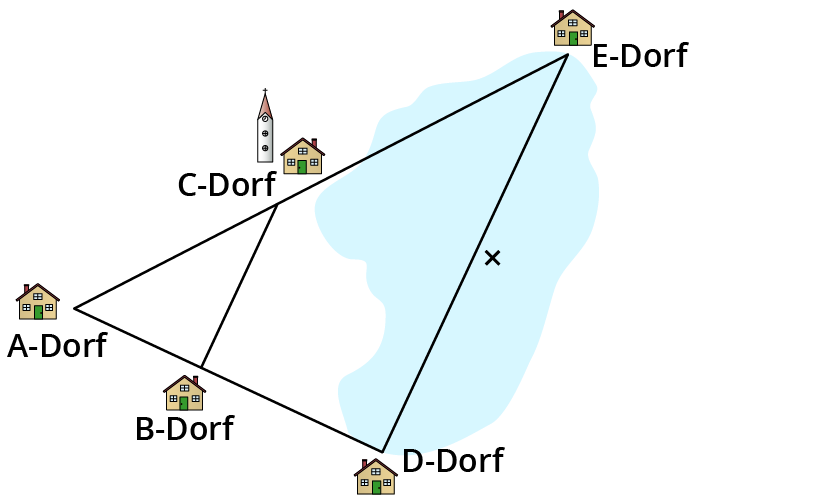
Den Strahlensatz benötigst du zum Beispiel in der Landvermessung oder in dem Försterbetrieb. Mithilfe von Strahlensätzen kannst du Streckenlängen bestimmen - zum Beispiel die Baumhöhe oder die Flussbreite.

Bild: iStockphoto.com (Mordolff)

Unterscheidung der Strahlensätze

Der 1. Strahlensatz gibt Streckenverhältnisse auf 2 Strahlen wieder.

Der 2. Strahlensatz bezieht einen Strahl und die Parallelen mit ein.

In beiden Fällen kannst du diese Strahlensatzgleichung verwenden.

oder

$$bar(ZB)/bar(ZA) = bar(ZB’)/bar(ZA’)$$ (1. Strahlensatz)

$$bar(AB)/bar(ZA) = bar(A’B’)/bar(ZA’)$$ (2. Strahlensatz)

Die beiden kurzen Teilstücke werden mit den beiden langen Teilstücken verglichen. Diese Verhältnisgleichung kannst du umstellen. Geschickt ist, wenn immer die gesuchte Strecke im Zähler steht.

Aufgaben mit Strahlensätzen

So gehst du vor:

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendest.
2) Stelle die Verhältnisgleichung auf.
3) Rechne die gesuchte Strecke aus.

Beispiel:

$$x$$ und $$y$$ sind gesucht.

$$x$$ berechnen:

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendst.
Um $$x$$ zu berechnen, kannst du nur den 2. Strahlensatz anwenden.

2) Stelle die Verhältnisgleichung auf.
$$x/bar(AB)=bar(ZB’)/bar(ZB)$$

3) Rechne die gesuchte Strecke aus.
$$x/4=10/5$$ $$|*4$$   Achtung, hier wird die Gesamtstrecke eingesetzt!$$5+5=10$$

$$x=(10*4)/5=8$$ $$cm$$

$$y$$ berechnen:

1) Entscheide, ob du den 1. oder den 2. Strahlensatz verwendst.
Jetzt kannst du für die Berechnung von $$y$$ den 1. oder 2. Strahlensatz verwenden. Hier ist der 1. Strahlensatz benutzt.

2) Stelle die Verhältnisgleichung auf.
$$(y+bar(ZA))/bar(ZA)=bar(ZB’)/bar(ZB)$$   Achtung: Verwende die Gesamtstrecke!

3) Rechne die gesuchte Strecke aus.
$$(y+3)/3=10/5$$ $$|*3$$

$$y+3=(10*3)/5=6$$ $$|-3$$

$$y=3$$ $$cm$$

So geht es mit dem erweiterten Strahlensatz

Du kannst auch mit dem erweiterten Strahlensatz $$y$$ ausrechnen.

$$y/bar(BB’)=bar(ZA)/bar(ZB)$$

$$y/5=3/5$$ $$|*5$$

$$y=(3*5)/5$$ $$|$$ Kürzen

$$y=(3*1)/1=3$$

Strahlensatzfiguren und andere geometrische Figuren

Es kommt noch besser: Du kannst den Strahlensatz benutzen, um Strecken in Rechtecken auszurechnen. Bestimme zuerst, wo deine Strahlensatzfigur liegt.

Berechne hier die Strecke $$b’$$.

$$(b’)/b=(a’)/a$$

$$(b’)/4=18/6$$ $$|*4$$

$$b’=(18*4)/6$$ $$|$$Kürzen

$$b’=(3*4)/1=12$$ $$cm$$

Die doppelte Strahlensatzfigur

Bei manchen Aufgaben liegen mehrere Strahlensätze vor.

$$f$$ $$||$$ $$g$$ $$||$$ $$h$$ und $$bar(ZB’’)$$ $$||$$ $$bar(AD)$$

$$bar(ZA)=2,6$$ $$cm$$ $$bar(BB’)=1,6$$ $$cm$$
$$bar(A A’)=1,3$$ $$cm$$ $$bar(AB)=1,7$$ $$cm$$
$$bar(A’ A’’)=3,8$$ $$cm$$ $$bar(A’B’)=2,5$$ $$cm$$
$$bar(ZB)=3,2$$ $$cm$$ $$bar(CB’)=1,7$$ $$cm$$

Gesucht sind hier die Strecken $$bar(A’’D)$$ und $$bar(B’B’’)$$. Für die Strecke $$bar(A’’D)$$ verwendest du den 2. Strahlensatz.

$$bar(ZA)=2,6$$ $$cm$$ $$bar(BB’)=1,6$$ $$cm$$
$$bar(A A’)=1,3$$ $$cm$$ $$bar(AB)=1,7$$ $$cm$$
$$bar(A’ A’’)=3,8$$ $$cm$$ $$bar(A’B’)=2,5$$ $$cm$$
$$bar(ZB)=3,2$$ $$cm$$ $$bar(CB’)=1,7$$ $$cm$$

$$bar(A’’D)/bar(A’C)=bar(A A’’)/bar(A A’)$$

Nebenrechnung:

$$bar(A’C)=2,5-1,7=0,8$$

$$bar(A A’’)=1,3+3,8=5,1$$

$$bar(A’’D)/(0,8)=(5,1)/(1,3)$$ $$|*0,8$$

$$bar(A’’D)=3,1$$ $$cm$$

Für die Strecke $$bar(B’B’’)$$ verwendest du den 1. Strahlensatz.

$$bar(B’B’’)$$ kannst du nicht direkt berechnen.
Aber das geht mithilfe von $$bar(ZB’’)$$!

$$bar(ZA)=2,6$$ $$cm$$ $$bar(BB’)=1,6$$ $$cm$$
$$bar(A A’)=1,3$$ $$cm$$ $$bar(AB)=1,7$$ $$cm$$
$$bar(A’ A’’)=3,8$$ $$cm$$ $$bar(A’B’)=2,5$$ $$cm$$
$$bar(ZB)=3,2$$ $$cm$$ $$bar(CB’)=1,7$$ $$cm$$

Hieraus kannst du $$bar(B’B’’)$$ berechnen:

$$bar(ZB’’)/bar(ZB’)=bar(ZA’’)/bar(ZA’)$$

Nebenrechnung:

$$bar(ZA’’)=2,6+1,3+3,8=7,7$$

$$bar(Z A’)=2,6+1,3=3,9$$

$$bar(Z B’)=3,2+1,6=4,8$$

$$bar(ZB’’)/(4,8)=(7,7)/(3,9)$$ $$|*4,8$$

$$bar(ZB’’)=9,5$$

$$bar(B’B’’)=bar(ZB’’)-bar(ZB’)=9,5-4,8=4,7$$ $$cm$$

Bei diesen Aufgaben gibt es oft mehrere Wege, die zum Ergebnis führen. Dieses sind nur 2 Beispiele.