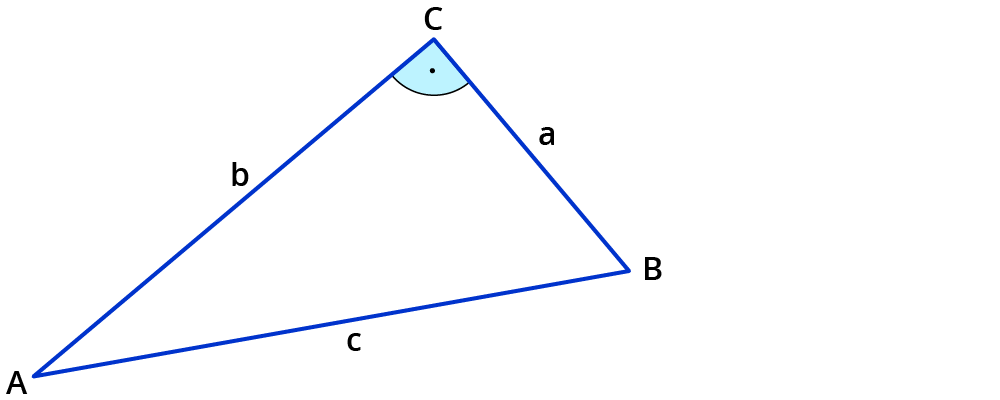
Berechnungen in rechtwinkligen Dreiecken

Um in rechtwinkligen Dreiecken zu rechnen, brauchst du diese Begriffe:

• Höhenwinkel (Neigungswinkel)
• Tiefenwinkel

Höhenwinkel oder Neigungswinkel

Stelle dir vor, du stehst an Punkt B. Der Höhenwinkel geht dann „nach oben“ auf.

Tiefenwinkel

Stelle dir vor, du stehst an Punkt C. Der Tiefenwinkel geht dann „nach unten“ auf.

So berechnest du den Höhenwinkel

Beispiel:

Unter welchem Höhenwinkel sieht man aus einer Entfernung von $$1,5$$ $$km$$ das Ulmer Münster $$(h=161$$ $$m)$$?

So geht’s:

Gesucht ist der Winkel $$beta$$. Du berechnest ihn über den Tangens:

$$tan beta = b/c$$

$$tan beta = 161/1500$$

$$beta approx 6,13^°$$

Man sieht das Ulmer Münster unter einem Höhenwinkel von $$6,13^°$$.

Bild: iStockphoto.com (Vladimir Khirman)

So rechnest du mit dem Tiefenwinkel

Beispiel:

Von einem $$64$$ $$m$$ hohen Leuchtturm sieht man ein Schiff unter dem Tiefenwinkel $$epsilon = 14,7^°$$. Wie weit ist das Schiff vom Leuchtturm entfernt?

So geht’s

Gesucht ist die Seitenlänge $$c$$. Du berechnest sie über den Tangens:

$$tan beta = b/c$$   $$|*c$$

$$c * tan beta = b$$       $$|:tan beta$$

$$c = b/(tan beta)$$

$$c = 64/(tan 14,7^°)$$

$$c approx 243,95   m$$

Das Schiff ist rund $$243,95$$ $$m$$ vom Leuchtturm entfernt.

Bild: fotolia.com (Brigitte Wegner)