Mit Sinus, Kosinus, Tangens im rechtwinkligen Dreieck rechnen
Das rechtwinklige Dreieck
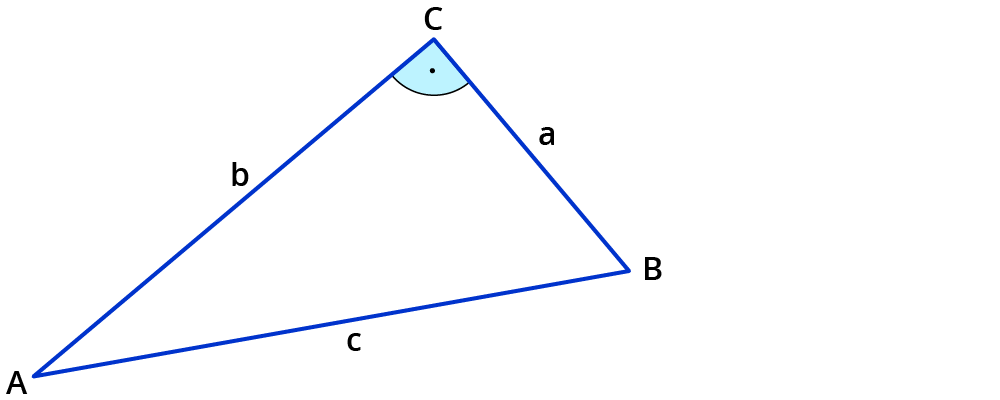
Bezeichnungen im rechtwinkligen Dreieck

Die längste Seite im rechtwinkligen Dreieck liegt dem rechten Winkel gegenüber. Sie heißt Hypotenuse.
Die beiden übrigen Seiten heißen Katheten.
Gegenkathete und Ankathete
Die Katheten werden noch einmal unterschieden.

Die Kathete, die dem Winkel α gegenüber liegt, heißt Gegenkathete von α.
Die Kathete, die am Winkel α anliegt, heißt Ankathete von α.
Beispiel:

Seite a:
Da die Seite a dem Winkel α gegenüberliegt, ist die Seite a die Gegenkathete des Winkels α. Da die Seite a aber auch am Winkel β anliegt, ist sie gleichzeitig die Ankathete von β.
Seite b:
Da die Seite b dem Winkel β gegenüberliegt, ist die Seite b die Gegenkathete des Winkels β. Da die Seite b aber auch am Winkel α anliegt, ist sie gleichzeitig die Ankathete von α.
Trigonometrie
Jetzt wird gleich gerechnet. Der Teil der Mathematik, in dem Seiten und Winkel in Dreiecken berechnet werden, heißt Trigonometrie. Los geht es mit rechtwinkligen Dreiecken.

In rechtwinkligen Dreiecken kannst du gleiche Längenverhältnisse entdecken.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Der Sinus eines Winkels

a) α=30°; a=2 cm; c=4 cm
b) α=30°; a=3 cm; c=6 cm
Der Quotient ac=GegenkatheteHypotenuse hat bei beiden rechtwinkligen Dreiecken den gleichen Wert.
a) ac=24=12
b) ac=36=12
Dieses Längenverhältnis wird Sinus genannt.
Im rechtwinkligen Dreieck gilt:
Sinus=GegenkatheteHypotenuse
Der Kosinus eines Winkels
Der Quotient bc=AnkatheteHypotenuse hat bei beiden rechtwinkligen Dreiecken den gleichen Wert.
Dieses Längenverhältnis wird Kosinus genannt.
Im rechtwinkligen Dreieck gilt:
Kosinus=AnkatheteHypotenuse
Der Tangens eines Winkels
Der Quotient ab=GegenkatheteAnkathete hat bei beiden rechtwinkligen Dreiecken den gleichen Wert.
Dieses Längenverhältnis wird Tangens genannt.
Im rechtwinkligen Dreieck gilt:
Tangens=GegenkatheteAnkathete

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Einfache Berechnungen mit den Winkelfunktionen
Beispiel 1: Seiten berechnen

gegeben: c=4 cm; α=30°; γ=90°
Seite a
1. Formel aufstellen
sinα=GegenkatheteHypotenuse ∣⋅c
2. Formel umstellen
sinα=GegenkatheteHypotenuse ∣⋅c
c⋅sinα=a
3. Ausrechnen
4⋅sin30°=a
2 cm=a
Seite b
1. Formel aufstellen
cosα=AnkatheteHypotenuse ∣⋅c
2. Formel umstellen
cosα=AnkatheteHypotenuse ∣⋅c
c⋅cosα=b
3. Ausrechnen
4⋅cos30°=b
3,46cm≈b
TR-Eingabe:
TR-Eingabe:
Einfache Berechnungen mit den Winkelfunktionen
Beispiel 2: Winkel berechnen

a=3 cm; b=4 cm; α=?
Winkel α
1. Formel aufstellen
tanα=GegenkatheteAnkathete=ab
2. Ausrechnen
tanα=34
α≈36,87°
TR-Eingabe:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen