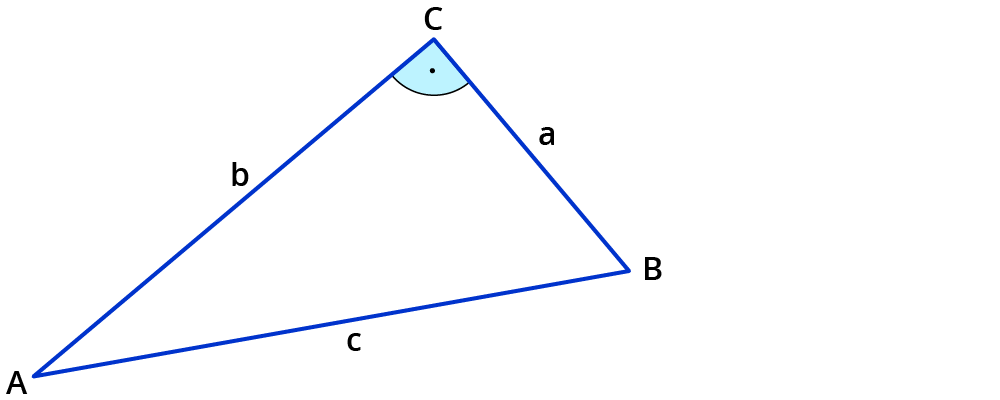
Mit Sinus, Kosinus, Tangens in gleichschenkligen und gleichseitigen Dreiecken rechnen
Gleichschenklige Dreiecke

Zwei Seiten (Schenkel) sind gleich groß. Die dritte Seite heißt Basis.
Die beiden Winkel an der Basis heißen Basiswinkel und sind gleich groß.
Die Höhe auf die Basis halbiert die Basisseite und den Winkel über der Basis.
Berechnungen im gleichschenkligen Dreieck
Bis jetzt hast du nur in einem rechtwinkligen Dreieck gerechnet. Sinus, Kosinus und Tangens lassen sich auch nur in rechtwinkligen Dreiecken anwenden.
Im allgemeinen gleichschenkligen Dreieck gibt es keinen rechten Winkel. Du erzeugst einen rechten Winkel, indem du die Höhe auf die Basis einzeichnest.
Es gilt:
a=b α=β x=y=c2

Beispiel:
Gegeben ist ein gleichschenkliges Dreieck mit a=b=5 cm, α=50°.
Berechne den Winkel γ und die Länge der Basis c.
γ=180°-2⋅50°
γ=80°
Jetzt berechnest du die Strecke x:
cosα=xb ∣⋅b
b⋅cosα=x
5⋅cos50°=x
3,21 cm =x
x ist die Hälfte der Basis c. Also c=3,21⋅2=6,42 cm.
Gleichseitige Dreiecke

In gleichseitigen Dreiecken sind alle Seiten gleich lang und alle Winkel gleich groß.
a=b=c x=y=c2 α=β=γ
Um ein rechtwinkliges Dreieck zu erhalten, zeichnest du wieder eine Höhe ein. Sie halbiert die Seite, weil es ein gleichseitiges Dreieck ist.
Beispiel:
Gegeben ist ein gleichseitiges Dreieck mit hc=5 cm, α=60°. Berechne die Länge der Seite a.
sinα=hca ∣⋅a
a⋅sinα=hc |sinα
a=hcsinα
a=5sin60°
a=5,77 cm

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen