Rechnen mit Sinus, Kosinus und Tangens

Wenn du viel mit Sinus, Kosinus und Tangens gerechnet hast, bist du jetzt fit für eine bunte Mischung von Anwendungen.

Hier siehst du im Überblick alle Berechnungen:

Im rechtwinkligen Dreieck gilt:

`sin alpha = (Geg\enkathete) / (Hypoten\use)`

`cos alpha = (Ankathete) / (Hypoten\use)`

`tan alpha = (Geg\enkathete) / (Ankathete)`

In beliebigen Dreiecken gilt:

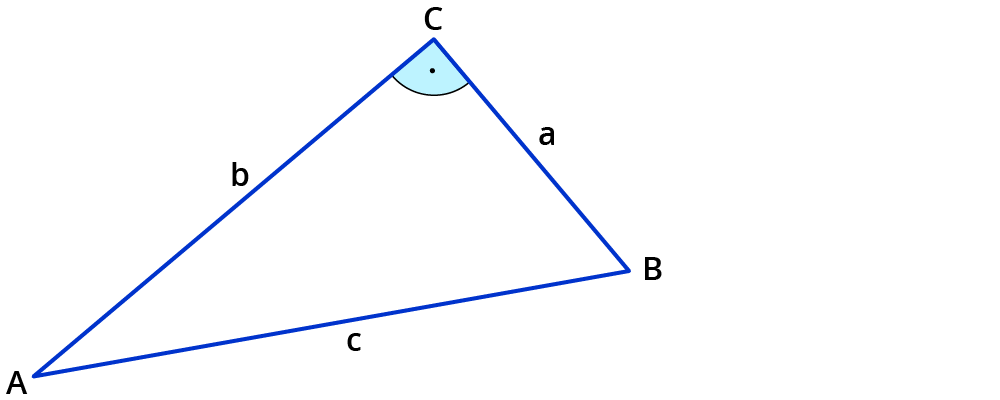
Der Sinussatz
`a/sin alpha = b/sin beta`   `a/sin alpha = c/sin gamma`   `b/sin beta = c/sin gamma`

Der Kosinussatz
`a^2=b^2+c^2-2*b*c*cos alpha`

`b^2=a^2+c^2-2*a*c*cos beta`

`c^2=a^2+b^2-2*a*b*cos gamma`

Rechtwinklige Dreiecke erzeugen

Beliebige Dreiecke kannst du in 2 rechtwinklige Dreiecke zerlegen oder zu einem rechtwinkligen Dreieck ergänzen. Dazu zeichnest du eine Höhe ins Dreieck ein.

Halt, aber eine Besonderheit gibt es noch.

Berechnen von Steigungen

Kennst du dieses Verkehrszeichen? Es zeigt die Steigung oder das Gefälle in den Bergen an.

Bild:fotolia.com (AK-DigiArt)

Mithilfe des Tangens kannst du berechnen, in welchem Winkel die Straße ansteigt.

Beispiel:

12 % Steigung heißt:
Auf 100 m horizontal gemessener Entfernung beträgt der Höhenunterschied 12 m.

Der Zusammenhang zwischen der Steigung `m` und dem Steigungswinkel `alpha` ist also

`m=tan alpha`

Der Winkel `alpha` wird mit dem Tangens berechnet.

`tan alpha=12/100`

`tan alpha=0,12`

`alpha=6,84^°`

Und andersrum

Beispiel 1: `m` gegeben `(m=16 %)`

`16%=0,16=16/100`

`m=16/100`

`tan alpha=m`

`tan alpha=16/100`

`alpha=9,09^°`

Beispiel 2: Winkel `alpha` gegeben `(alpha=5^°)`

`alpha=5^°`

`tan alpha=0,09` (auf 2 Nachkommastellen gerundet)

`m=0,09=9/100`

`m=9%`