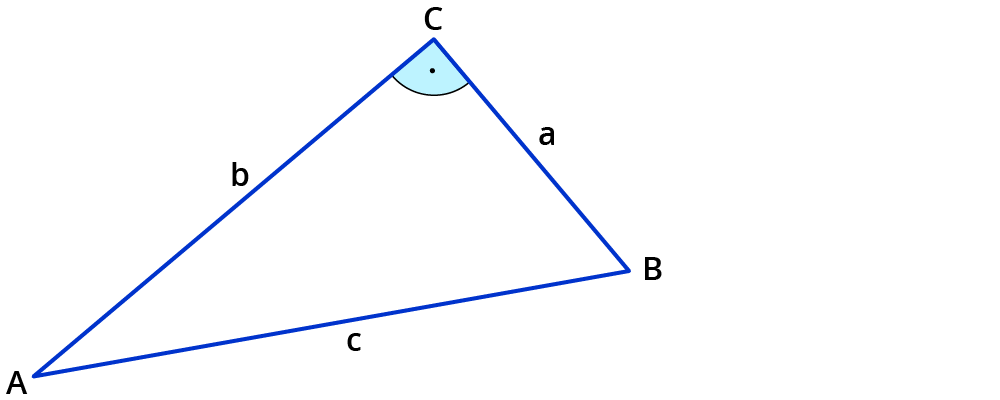
Den Kosinussatz anwenden
Der Kosinussatz

c=7 km, b=3,6 km, α=56,3°
Berechne die Seite a.
Hm, den Sinussatz kannst du mit den gegebenen Stücken nicht anwenden.
Aber es gibt da noch einen Satz - den Kosinussatz!
Die Herleitung

Zeichne die Höhe ein, um rechtwinklige Dreiecke zu erzeugen.
Dreieck ADC
cosα=yb ∣⋅b
b⋅cosα=y
Rechtwinkliges Dreieck DBC (Satz des Pythagoras)
h2c+x2=a2 ∣x=c-y
h2c+(c-y)2=a2 ∣-(c-y)2
h2c=a2-(c-y)2
Rechtwinkliges Dreieck ADC (Satz des Pythagoras)
h2c+y2=b2 ∣-y2
h2c=b2-y2
Gleichsetzen von h2c
a2-(c-y)2 = b2-y2 ∣+(c-y)2
a2=b2-y2+(c-y)2
a2=b2-y2+c2-2cy+y2
a2=b2+c2-2⋅c⋅ y
a2=b2+c2-2⋅c⋅ b⋅cosα
Das ist eine Gleichung des Kosinussatzes.
Kosinussatz
In jedem Dreieck gilt:
a2 =b2+c2-2⋅b⋅c⋅cosα
b2 =a2+c2-2⋅a⋅c⋅cosβ
c2 =a2+b2-2⋅a⋅b⋅cosγ
Seite und zugehöriger Winkel stehen immer außen.
Ein Beispiel
Jetzt kannst du die Seite a des Dreiecks zu Beginn berechnen.

c=7 km, b=3,6 km, α=56,3°
Setze die gegebenen Stücke in den Kosinussatz ein:
a2=3,62+72-2⋅3,6⋅7⋅cos56,3°
a2=34 ∣√
a=5,83 km
Der Kosinussatz:
a2 =b2+c2-2⋅b⋅c⋅cosα
b2 =a2+c2-2⋅a⋅c⋅cosβ
c2 =a2+b2-2⋅a⋅b⋅cosγ

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen