Den Sinussatz anwenden
Sinus in beliebigen Dreiecken?
Bisher hast du mit Sinus, Kosinus und Tangens nur im rechtwinkligen Dreieck gerechnet. In beliebigen Dreiecken hast du durch das Einzeichnen einer Höhe rechtwinklige Dreiecke hergestellt. Dann konntest du wieder mit Sinus, Kosinus und Tangens rechnen.
Aber es gibt eine Regel, mit der du mithilfe des Sinus in jedem Dreieck die Seitenlängen und Winkel berechnen kannst!
Das ist der Sinussatz. Den kannst du dir sogar selbst herleiten.
Herleiten des Sinussatzes
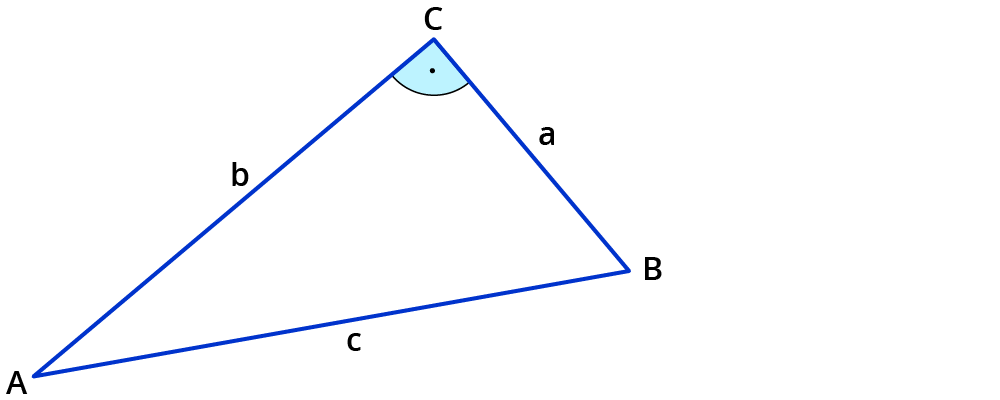
Nimm ein beliebiges Dreieck und zeichne eine Höhe ein.
$$a=165$$ $$m$$, $$alpha=40^°$$, $$beta=60^°$$, $$b=?$$
$$sin alpha = h_c/b$$ $$|*b$$
$$b*sin alpha= h_c$$
$$sin beta= h_c/a$$ $$|*a$$
$$a*sin beta= h_c$$
Gleichsetzen von $$h_c$$
$$b*sin alpha$$ $$=$$ $$a*sin beta$$ $$|: sin alpha$$
$$b=(a*sin beta)/sin alpha$$ $$|:sin beta$$
Also gilt:
$$b/sin beta = a/sin alpha$$
Wenn das nicht nach einer tollen Formel zum Rechnen aussieht!
$$b*sin alpha$$ ist so lang wie $$h_c$$.
Und $$a*sin beta$$ ist so lang wie $$h_c$$.
Also müssen $$b*sin alpha$$ und $$a*sin beta$$ gleich lang sein. Mathematisch bedeutet das „Gleichsetzen“:
$$b*sin alpha = a*sin beta$$.
Der Sinussatz
Die Rechnung von eben kannst du mit jeder der 3 Höhen des Dreiecks durchführen. Dann ergibt sich:
In jedem Dreieck gilt:
$$a/sin alpha = b/sin beta$$ $$a/sin alpha = c/sin gamma$$ $$b/sin beta = c/sin gamma$$
Zum Rechnen nimmst du dir nur eine der Gleichungen. Und welche? Das hängt von der Aufgabe ab: Du musst 3 der Variablen (Unbekannten) gegeben haben, damit du weißt, welche Gleichung du anwendest.
Wenn du die Gleichungen umstellst, erhältst du diese Formen:
$$ a/b=sin alpha/sin beta$$ $$b/c=sin beta / sin gamma$$ $$a/c=sin alpha / sin gamma$$
Du kannst dir aussuchen, wie du dir den Sinussatz am besten merkst.
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispiel 1: Gesuchte Größe im Zähler
$$a=165$$ $$m$$, $$alpha=40^°$$, $$beta=60^°$$, $$b=?$$
Lösung
Bestimme anhand der gegebenen Stücke, welche Gleichung des Sinussatzes du nimmst:
$$a/sin alpha=b/sin beta$$
Stelle die Gleichung um und berechne:
$$a/sin alpha=b/sin beta$$ $$|*sin beta$$
$$(a*sin beta)/sin alpha=b$$
$$(165*sin 60^°)/sin 40^° = b$$
$$222,30$$ $$m$$ $$=b$$
Beispiel 2: Gesuchte Größe im Nenner
$$b=5,7$$ $$cm$$, $$c=7,8$$ $$cm$$, $$gamma=43^°$$, $$beta=?$$
Lösung
Bestimme anhand der gegebenen Stücke, welche Gleichung des Sinussatzes du nimmst:
$$b/sin beta=c/sin gamma$$
Vertausche Zähler und Nenner auf beiden Seiten der Gleichung. Stelle um und berechne:
$$sin beta/b=sin gamma/c$$ $$|*b$$
$$sin beta=(sin gamma *b)/c$$
$$sin beta = (sin 43^° * 5,7)/7,8$$
$$ beta=29,89^°$$
Wenn die gesuchte Größe im Nenner steht, bildest du am besten auf beiden Seiten der Gleichung den Kehrwert (Zähler und Nenner vertauschen). Dann kannst du wie gewohnt weiterrechnen.
Auf 2 Nachkommastellen gerundet erhältst du $$sin beta= 0,5$$. Rechnest du mit diesem gerundeten Ergebnis weiter, bekommst du $$beta=30^°$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
