Erinnerung: Die Quadratwurzel

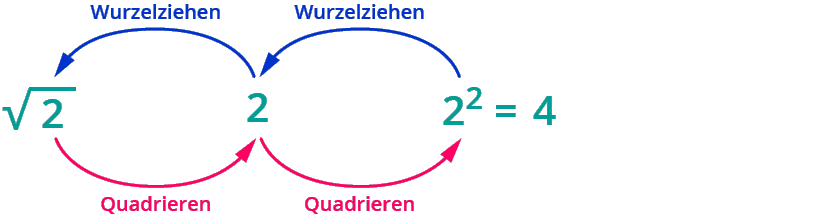
Du kennst schon die Quadratwurzel. Sie ist die „Umkehrung“ von „hoch 2“.

$$sqrt121= 11$$, denn $$11^2 = 11 cdot 11 = 121$$

Die Wurzel von $$x$$ ist die nicht-negative Zahl, die mit sich selbst multipliziert wieder $$x$$ ergibt.

Was ist die 3. Wurzel?

Du kannst nicht nur „hoch 2“, sondern auch „hoch 3“ umkehren! Dazu brauchst du die 3. Wurzel, oder „Kubikwurzel“.

$$root 3 (8)= 2$$, denn $$2^3 = 2*2*2 = 8$$

3. Wurzel

$$uarr$$

$$root 3(8)=2$$

$$darr$$

Radikand

Geometrisch

Quadrat

Den Flächeninhalt eines Quadrats berechnest du mit $$A=a^2$$. Dabei ist $$a$$ die Seitenlänge.
Also gilt umgekehrt: $$sqrtA=a$$

Die Wurzel des Flächeninhaltes $$A=9$$ des Quadrates ist die Seitenlänge $$a=3$$.
$$sqrt 9 = 3$$, denn $$3^2=9$$.

Würfel

Wie kriegst du die Seitenlänge eines Würfels raus?

Das Volumen $$V$$ eines Würfels berechnest du mit $$V=a^3$$. Also gilt $$root (3)V=a$$.

Die 3. Wurzel des Volumens $$V=8$$ des Würfels ist die Seitenlänge $$2$$.
$$root 3 (8)= 2$$, denn $$2^3 = 8$$

Ein paar Beispiele

$$root 3 (1)=1$$, denn $$1^3=1$$

$$root 3 (8)=2$$, denn $$2^3=8$$

$$root 3 (27)=3$$, denn $$3^3=27$$

$$root 3 (64)=4$$, denn $$4^3=64$$

$$root 3 (125)=5$$, denn $$5^3=125$$

$$root 3 (1 000)=10$$, denn $$10^3=1000$$

Jetzt auch mit Komma

Auch Dezimalzahlen haben Kubikwurzeln:

$$root 3 (3,375)=1,5$$

$$root 3 (0,125)=0,5$$

$$root 3 (0,001)=0,1$$

$$root 3 (15,625)=2,5$$

Und Brüche

$$root 3(8/27)=2/3$$, denn $$(2/3)^3=2/3*2/3*2/3=8/27$$

$$root 3(1/125)=1/5$$, denn $$(1/5)^3=1/5*1/5*1/5=1/125$$

Irrational?

Du hast jetzt eine Menge 3. Wurzeln gesehen, die natürliche Zahlen sind (64) oder Dezimalzahlen (0,5) oder Brüche. Die meisten 3. Wurzeln sind allerdings irrational, das heißt nicht-abbrechende, nicht-periodische Dezimalzahlen.

Beim Berechnen hilft dir der Taschenrechner. Suche die Taste für die 3. Wurzel und tippe ein:

$$root 3(x)$$ $$ 15$$
oder
 $$ 15$$$$root 3(x)$$

und der Taschenrechner gibt dir $$2,4662120743…$$ aus. Die Anzahl der Nachkommastellen kann verschieden sein, je nachdem, wie viel Platz auf deinem Display ist.
Meist sollst du auf 2 Nachkommastellen runden:
$$root 3(15) approx 2,47$$

Buchstabensalat

Du ahnst es schon: Was mit Zahlen geht, geht auch mit Variablen.:-) Bei Variablen muss bloß immer dabei stehen, welche Zahlen du einsetzen kannst.

Beispiele:

$$root 3 (x^3)=x$$ - mit $$x ge0$$

$$root 3 (x^6)= x^2$$, denn $$(x^2)^3=x^6$$ - mit $$x ge0$$

$$root 3 (1/y^6)= 1/y^2$$, denn $$(1/y^2)^3=1^3/((y^2)^3) = 1/y^6$$ - mit $$y ge0$$

Intervallschachtelung

Mit der Intervallschachtelung kannst du die 3. Wurzel näherungsweise berechnen, ohne die Wurzeltaste deines Taschenrechners zu benutzen.

Beispiel: $$root 3 (52)$$

Hinweis: Die blau markierten Rechenschritte berechnest du mit dem Taschenrechner.

1. Schritt: Das erste Intervall finden

Zwischen welchen natürlichen Zahlen liegt $$root 3 (52)$$?

• Probiere es mit den Kubikzahlen $$1^3$$, $$2^3$$, $$3^3$$, $$4^3, … $$ aus.
• Es gilt $$3^3 = 27 le 52 le 4^3 = 64$$. Also liegt $$root 3 (52)$$ zwischen $$3$$ und $$4$$.

2. Schritt: Schachtele das Intervall weiter ein

• Füge eine Nachkommastelle an.
• Probiere mit dem Taschenrechner, zwischen welchen der Zahlen $$(3,1)^3, (3,2)^3, (3,3)^3, …, (3,9)^3$$ die Zahl $$52$$ liegt.
• $$3,7leroot 3 (52)le3,8$$ , weil $$(3,7)^3=50,65$$$$le52le$$$$(3,8)^3=54,87$$

3. Schritt: Zwei Nachkommastellen

• Berechne mit dem Taschenrechner, zwischen welchen der Zahlen $$(3,71)^3, (3,72)^3, (3,73)^3, …, (3,79)^3$$ die Zahl $$52$$ liegt.
• $$3,73leroot 3 (52)le3,74$$ , weil $$(3,73)^3=51,9$$$$le52le$$$$(3,74)^3=52,31$$

3. Schritt: Drei Nachkommastellen

• Finde mit dem Taschenrechner heraus, zwischen welchen der Zahlen $$(3,731)^3, (3,732)^3, (3,733)^3, …, (3,739)^3$$ die Zahl $$52$$ liegt.
• $$3,732leroot 3 (52)le3,733$$ , weil $$(3,732)^3=51,98$$$$le52le$$$$(3,733)^3=52,02$$

Mit jedem Schritt grenzt du $$root 3 (52)$$ genauer ein. Da $$root 3 (52)$$ irrational ist, erhältst du aber niemals den exakten Wert.