n-te Wurzeln berechnen
Wurzeln, Wurzeln
Du kennst
- die Quadratwurzel: $$root 2(16)=4$$, denn $$4^2=16$$
- die 3. Wurzel: $$root 3(27)=3$$, denn $$3^3=27$$
Und? Gibt es auch eine 4. und 5. Wurzel? Ja!
Das ist die Umkehrung von „hoch 4“ und „hoch 5“.
Das kannst du theoretisch unendlich fortsetzen. Um das gut aufschreiben zu können, nehmen Mathematiker - natürlich :-) - eine Variable: n.
Die n-te Wurzel schreibst du so: $$root n ( )$$
Für n kannst du jede beliebige natürliche Zahl einsetzen.
Die natürlichen Zahlen $$NN$$ sind $${0;1;2;3;…}$$
Beispiele
- $$root 4 (625)=5$$, denn $$5^4=625$$
- $$root 5 (243)=3$$, denn $$3^5=243$$
- $$root 10 (1024)=2$$, denn $$2^10=1024$$
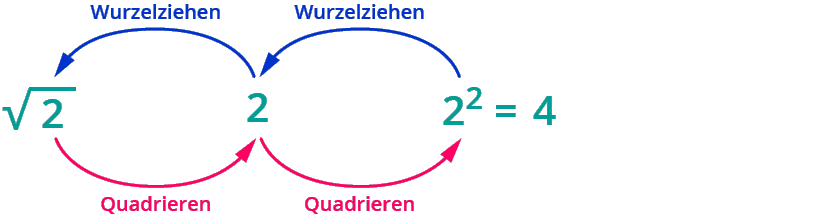
Das Wurzelziehen ist die Umkehrung des Potenzierens. Für jede natürliche Zahl $$n$$ gilt: $$root n (x^n)=x$$
Mit Taschenrechner und krummen Zahlen
Bei höheren Wurzeln wirst du oft den Taschenrechner brauchen. Die Taschenrechner funktionieren unterschiedlich, aber die häufigste Tasten-Kombination ist diese hier.
So tippst du $$root 4 (625)$$ ein:
4
shift oder inf
wo klein drüber steht: $$rootn(x)$$
$$625$$
$$=$$
Da kommen auch mal irrationale Zahlen raus:
$$root 6 (8)=1,41421356237… approx 1,41$$
Die Bezeichnung der Taste der n-ten Wurzel sieht auf jedem Taschenrechner-Modell ein bisschen anders aus:
$$root y(x)$$ oder
$$root x ( )$$
Irrationale Zahlen kannst du nicht als Brüche darstellen. Sie haben unendlich viele Nachkommstellen und sind nicht periodisch.
Eine Aufgabe zum Schluss
Als Aufgabenstellung kann dir begegnen:
Berechne $$root n 64$$ für die Zahlen $$n=2,3,5$$.
Du setzt nacheinander für n die Zahlen 2 und 3 und 5 ein.
- $$root 2 64=8$$, denn $$8^2=64$$
- $$root 3 64=4$$, denn $$4^3=64$$
- $$root 5 64 approx 2,297$$, berechnet mit dem Taschenrechner
Die ganz normale Quadratwurzel ist also auch eine $$n$$-te Wurzel, mit $$n=2$$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
