Potenzen mit gebrochenen Exponenten
Neue Exponenten
23, (-25)2, x-2, (14)2, 1,5-1
Diese Potenzen sind dir vertraut: verschiedene Zahlen als Basis und positive und negative ganze Zahlen als Exponent.
Aber: Die Exponenten können auch Brüche sein wie in 212!
Häh? 23=2⋅2⋅2, aber wie soll das mit einem Bruch gehen…
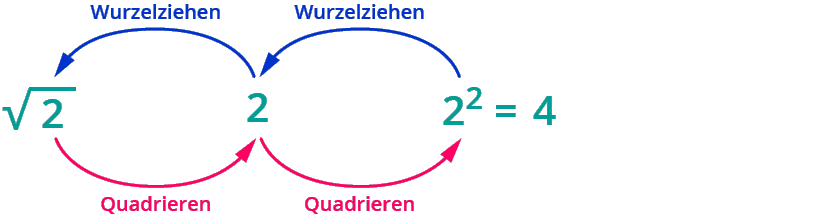
Das ist festgelegt über die Wurzel! Los geht’s:

Brüche 1n als Exponent
Mathematiker haben Potenzen mit Brüchen so festgelegt.
Beispiele:
- 412=2√4=2
- 6413=3√64=4
- 8114=4√81=3
- …
- 31n=n√3
„Hoch einhalb“ ist dasselbe wie das Ziehen der 2. Wurzel.
Allgemein: „Hoch 1 durch n“ ist dasselbe wie das Ziehen der n-ten Wurzel.
Für eine Zahl a gilt: a1n=n√a
Dabei ist a eine reelle Zahl größer 0, n ist eine natürliche Zahl größer 1.
Das heißt a∈ℝ und a>0; n∈ℕ und n>1.
Brüche mn als Exponent
Der Exponent kann aber auch ein anderer Bruch sein. Sieh dir den Term x67 an.
Wie soll das jetzt gehen?
x67
ist dasselbe wie:
x6⋅17
Potenzgesetze:
(x6)17
n-te Wurzel ziehen für n=7:
7√x6
Also: x67=7√x6
Für eine Zahl a gilt: amn=n√am
Dabei ist a eine reelle Zahl größer 0, n ist eine natürliche Zahl größer 1 und m ist eine ganze Zahl.
a∈ℝ und a>0; n∈ℕ und n>1; m∈ℤ.
Meistens berechnest du diese Potenzen bzw. Wurzeln mit dem Taschenrechner. Bei manchen Taschenrechner darfst du die Klammern nicht vergessen:
[Bild der Eingabe: x^(6/7)]
Und so geht’s allgemein:
xab
xa⋅1b
(xa)1b
b√xa

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Und in der Praxis?
Potenzen mit rationalen Exponenten kommen beim Bakterienwachstum vor.
Eine Bakterienart vermehrt sich so, dass sich ihre Anzahl nach einer Stunde vervierfacht.
| Zeit t in Stunden | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Anzahl x der Bakterien | 1 | 4 | 16 | 64 |
Fällt dir was an den Zahlen auf?
| Zeit t in Stunden | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Anzahl x der Bakterien | 40=1 | 41=4 | 42=16 | 43=64 |
Das kannst du in einer Formel schreiben: Anzahl Bakterien=4Anzahl Stunden oder kurz x=4t.
Mit der Formel kannst du die Anzahl der Bakterien nach einer halben Stunde berechnen. Jetzt kommt die Wurzel ins Spiel.
x=412=√4=2
Oder nach 2,5 Stunden?
x=42,5=452=45⋅(12)=(45)12=√45=√1024=32
Nach 2,5 Stunden gab es 32 Bakterien.
Für diese Rechnung brauchtest du schon ein paar Regeln aus der Bruchrechnung und Potenzgesetze wie (am)n=am⋅n.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen