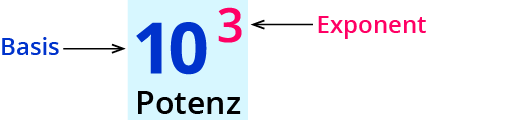Zehnerpotenzen mit ganzzahligen Exponenten
Zehnerpotenzen mit ganzzahligen Exponenten
Schwer überschaubar
Die Zahl 137589472 ist schwer zu lesen.
Du teilst die Ziffern in Dreiergruppen ein.
137 589 472
Jetzt kannst du sie besser lesen:
137 Millionen 589 Tausend 472
Du weißt schon, dass es besondere Namen für sehr große Zahlen gibt:
1 000 000 ist 1 Million
1 000 000 000 ist 1 Milliarde
1 000 000 000 000 ist 1 Billion
Warum gibt es eigentlich zehn Ziffern?
Unsere Zahlen werden im Zehnersystem aufgeschrieben - deshalb gibt es zehn verschiedene Ziffern.
Unser Zehnersystem (Dezimalsystem) ist ein Stellenwertsystem
Du weißt schon, wie eine Stellenwerttabelle aufgebaut ist und kannst die Zahl 137 589 472 dort eintragen:
| Mio | HT | ZT | T | H | Z | E |
|---|---|---|---|---|---|---|
| 137 | 5 | 8 | 9 | 4 | 7 | 2 |
Dir fällt auf: Von rechts nach links wird jeder Stellenwert gerade zehnmal so groß wie der vorige. Deshalb benötigst du die Ziffern Null bis Neun, beim zehnfachen Stellenwert rutschst du einfach eine Stelle nach links.
Die Stellenwerte sind Zehnerpotenzen
Jeden Stellenwert in unserem Zehnersystem kannst du als Potenz mit der Basis 10 darstellen.
Die Stellenwerte als Zehnerpotenzen
Du weißt schon:
$$100=10^2$$
$$1000=10^3$$
$$10 000=10^4$$
$$100 000=10^5$$ usw.
1 Million = $$10^6$$
1 Milliarde = $$10^9$$
1 Billion = $$10^12$$ usw.
Du kennst Potenzen als Produkte aus immer denselben Faktoren.
Für $$10*10*10$$ schreibst du $$10^3$$.
Eine Potenz sieht also immer so aus:
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Weiter im System
Bisher weißt du: Bei einer Potenz mit der Basis 10 gibt der Exponent die Anzahl der Nullen an.
Du kannst die Potenzschreibweise erweitern
Um das System fortzusetzen, schreibst du
$$10 =10^1$$
$$1= 10^0$$
$$0,1= 10^(-1)$$
$$0,01= 10^(-2)$$
$$0,001= 10^(-3)$$ usw.
Für Zehnerpotenzen gilt:
Positive Exponenten geben die Anzahl der Nullen hinter der 1 an.
Negative Exponenten geben die Position der 1 hinter dem Komma an.
Alte Bekannte ohne Komma
Wie du weißt, sind Dezimalzahlen nur eine besondere Schreibweise für Brüche mit Zehnerzahlen im Nenner.
Beispiele: $$0,001=1/1000$$ oder $$0,02=2/100$$
Die Nachkommastellen sind gleich der Anzahl der Nullen in der Zehnerzahl im Nenner des Bruchs.
Also gilt für die Zehnerpotenzen:
| $$10^(-1)=0,1=1/10=1/10^1$$ | ein Zehntel |
| $$10^(-2)=0,01=1/100=1/10^2$$ | ein Hundertstel |
| $$10^(-3)=0,001=1/1000=1/10^3$$ | ein Tausendstel |
| $$10^(-6)=0,000001=1/1000000=1/10^6$$ | ein Millionstel |
Zehnerpotenzen auf dem Taschenrechner
Sehr große bzw. sehr kleine Zahlen werden in der sogenannten wissenschaftlichen Schreibweise angezeigt.
Die wissenschaftliche Anzeige besteht aus einer Zahl mit einer Stelle vor dem Komma und einer Angabe des Exponenten.
Ausgeschrieben besteht die wissenschaftliche Schreibweise einer Zahl aus einer Zahl mit einer Stelle vor dem Komma, die mit der passenden Zehnerpotenz multipliziert wird.
$$3,45*10^11=345000000000$$
$$3,45*10^(-4)=0,000345$$
Für die wissenschaftliche Schreibweise gilt:
Bei positivem Exponenten zur Basis 10 verschiebst du das Komma um so viele Stellen nach rechts, wie der Exponent angibt. Wenn nötig, füllst du dabei Nullen auf.
Bei negativem Exponenten zur Basis 10 verschiebst du das Komma um so viele Stellen nach links, wie der Exponent angibt. Wenn nötig, füllst du dabei Nullen auf.
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
