Quadratische Gleichungen grafisch lösen
Quadratische Gleichungen grafisch lösen
In einer quadratischen Gleichung kommt die Variable in der zweiten Potenz und nicht höher vor.
Beispiele: x2=3; x2+2x-3=0; 0,5x2-3x=1,5
Meistens sollst du quadratische Gleichungen lösen. Du suchst Zahlen für die Variable, die die Gleichung erfüllen. Diese Zahlen heißen Lösungen. Alle Lösungen bilden die Lösungsmenge L.
Quadratische Gleichungen kannst du durch rechnerische Verfahren lösen oder durch grafische Verfahren die Lösungen näherungsweise bestimmen.
Zum grafischen Lösen bildet man aus dem quadratischen Term der Gleichung eine quadratische Funktion, dem linearen Teil eine lineare Funktion und bringt die Graphen dieser Funktionen zum Schnitt.
Wenn du quadratische Gleichungen grafisch löst, betrachtest du immer die Funktion x2 und eine lineare Funktion.
Normalform einer quadratischen Gleichung: x2+px+q=0
⇒ quadratische Funktion: Q(x)=x2
⇒ lineare Funktion: L(x)=-px-q
Grafische Lösungen sind immer Näherungslösungen!
Grafisches Lösungsverfahren
Lösungsschritte zum grafischen Lösen quadratischer Gleichungen:
Beispiel: 0=x2+2x-3
- Gleichung so umformen, dass auf einer Seite der lineare Teil und auf der anderen Seite der quadratische Teil steht.
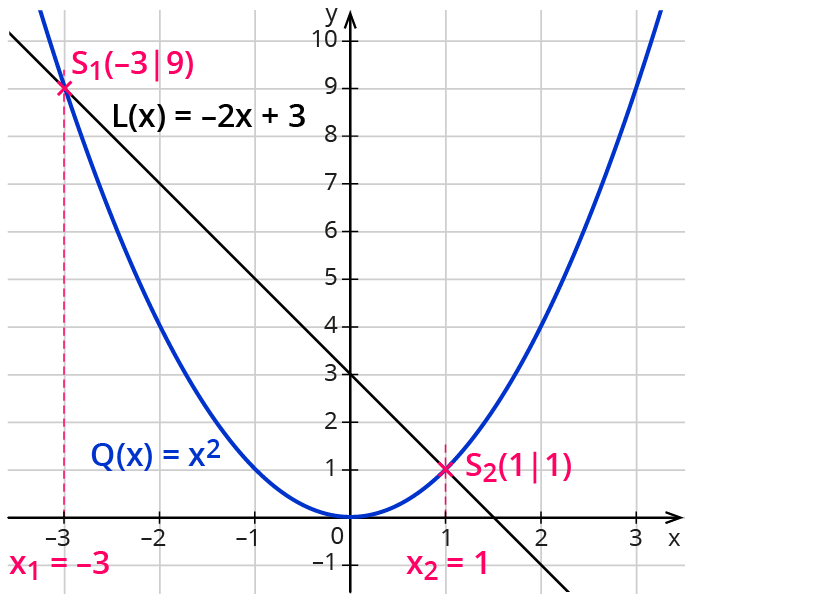
x2=-2x+3 - Terme als Funktionsterme einer quadratischen und einer linearen Funktion einsetzen.
Q(x)=x2 und L(x)=-2x+3 - Graphen der quadratischen Funktion (Normalparabel) und Graph der linearen Funktion (Gerade) in einem geeigneten Koordinatensystem zeichnen.

- Die x-Koordinaten der Schnittpunkte der Graphen sind die Lösungen der quadratischen Gleichung.
Lösungen: x1=-3 und x2=1
Lösungsmenge: L={-3∣1}
Die Lösungen der quadratischen Gleichungen ergeben sich aus den Schnittstellen (x-Koordinate) von x2 und der linearen Funktion.
Es gilt: Q(x)=L(x).
Einfache Gleichungen
Gleichungsart: 0=x2+q, q∈ℝ
Beispiel: 0=x2-6,25
1. Umformung: 0=x2-6,25 ∣+6,25
x2=6,25
2. Funktionsgleichungen: Q(x)=x2 und L(x)=6,25
3. Graphen von Q und L zeichnen:

4. Schnittstellen der Graphen
Lösungen der Gleichung: x1=-2,5 und x2=2,5
Lösungsmenge: L={-2,5∣2,5}
Lösungsfälle
- q>0: 2 Lösungen
- q=0: 1 Lösung
- q<0: keine Lösung
Graphen von L(x)=-q
Graph von L ist eine Gerade parallel zur x-Achse im Abstand von |-q|.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Noch ein Beispiel
Gleichungsart: 0=x2+px mit p∈ℝ
Beispiel: 0=x2+3x
1. Umformung: 0=x2+3x ∣-3x
x2=-3x
2. Funktionsgleichungen: Q(x)=x2 und L(x)=-3x
3. Graphen von Q und L zeichnen: 
4. Schnittstellen der Graphen
Lösungen der Gleichung: x1=-3 und x2=0
Lösungsmenge: L={-3;0}
Für alle p∈ℝ hat die Gleichung zwei Lösungen.
Die beiden Graphen schneiden sich im Koordinatenursprung.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen