Vermischte Aufgaben mit dem Dreisatz 2
Einsatz für den Dreisatz
Anna und Ben machen eine Ausbildung zum Hotelfachmann bzw. zur Hotelfachfrau. Dazu gehört auch, dass sie Vorräte für die Küche nachbestellen. Der Chefkoch gibt Folgendes bekannt:
Der Knoblauchvorrat des Hotels reicht 40 Tage, wenn täglich 1,6 kg verbraucht werden. Aufrgund einer Änderung der Speisekarte muss der Tagesverbrauch um 0,4 kg erhöht werden. Wie lange reicht der gleiche Vorrat?
Das berechnest du am einfachsten mit dem Dreisatz.

Zur Erinnerung
Der Dreisatz:
Wenn du eine gesuchte Größe nicht einfach mit den Angaben aus der Aufgabe berechnen kannst, ist ein Zwischenschritt über eine geeignete Größe notwendig. Das geht am einfachsten mit einer Tabelle.
Beispiel
Vier Zimmermädchen schaffen es, an einem Vormittag 20 Zimmer zu reinigen. Wie viele Zimmer können von fünf Zimmermädchen gereinigt werden?
| Zimmermädchen | Zimmer |
|---|---|
| 4 | 20 |
| 5 | ? |
Überlege dir eine Zahl als Zwischenschritt, auf die du
- leicht runterrechnen kannst und
- leicht auf den gesuchten Wert hochrechnen kannst.
| Zimmermädchen | Zimmer |
|---|---|
| 4 | 20 |
| 1 | 5 |
| 5 | ? |
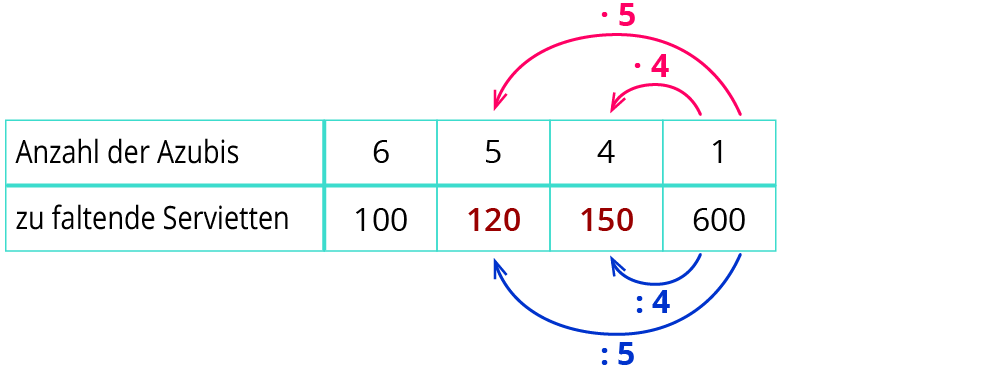
Bei proportionalen Zuordnungen (je mehr … desto mehr) musst du auf beiden Seiten der Tabelle mit der gleichen Zahl multiplizieren bzw. dividieren. → gleiche Faktoren
Bei antiproportionalen Zuordnungen (je mehr … desto weniger) musst du auf der einen Seite der Tabelle multiplizieren und auf der anderen Seite durch die gleiche Zahl dividieren. → gegensätzliche Faktoren
Dreisatz:
- Eine Tabelle erstellen.
- Eine geeignete Zwischengröße finden.
- Fehlende Größe berechnen.
Der Dreisatz heißt Dreisatz, weil er aus drei Rechenschritten (Sätzen) besteht.
Die Zahl 1 als Zwischenschritt funktioniert immer. Manchmal kann man aber mit anderen Zahlen einfacher rechnen.
Doppelt hält besser (zusammengesetzter Dreisatz)
Beim zusammengesetzten Dreisatz fließen mehr als zwei Bedingungen in die Rechnung ein.
Der Wäschezulieferer Herr Sauber erzählt den Hotelmitarbeitern ganz aufgeregt, dass seine Firma jetzt mehr Metallbänder produziert (mit denen die gereinigte Wäsche in Säcken auf den Paletten fixiert wird) obwohl ein Automat kaputt ist.
Beim zusammengesetzten Dreisatz rechnest du immer nur mit den Werten von zwei Spalten.
- Die mittlere Spalte vorerst nicht berücksichtigen.
- Mit den beiden übrigen Spalten rechnen.
- Erste Spalte und bereits Gerechnetes „wegdenken“. Rest berechnen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Und was passiert mit dem ganzen Knoblauch?
Um die Knoblauchaufgabe zu lösen, gehst du vor, wie beim einfachen Dreisatz:
1. Schritt: Eine Tabelle erstellen
Lies dabei die Aufgabenstellung genau, um die beiden Bezugsgrößen zu erkennen.
Der Knoblauchvorrat des Hotels reicht 40 Tage, wenn täglich 1,6 kg verbraucht werden. Aufgrund einer Änderung der Speisekarte muss der Tagesverbrauch um 0,4 kg erhöht werden. Wie lange reicht der gleiche Vorrat?

2. Schritt: Eine geeignete Zwischengröße finden
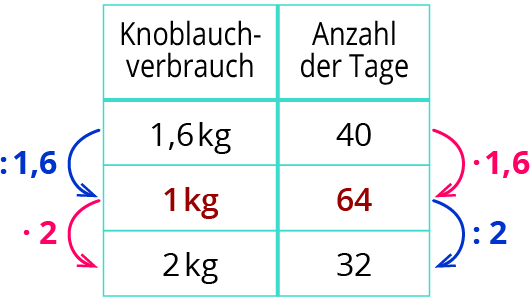
Als Zwischengröße bietet sich hier 0,2 kg an:

3. Schritt: Fehlende Größe berechnen
Da es sich um eine antiproportionale Zuordnung handelt, muss in der anderen Tabellenspalte mit den gegensätzlichen Faktoren gerechnet werden.

Wenn täglich 2 kg Knoblauch verbraucht werden, reicht der gleiche Vorrat also nur noch 32 Tage lang.
Hier ist ein Beispiel für die Berechnung mit der 1 als Zwischenschritt, aber ohne Taschenrechner ist die andere Version einfacher zu rechnen:
Jetzt wird es knifflig oder knobelig
Beispiel:
Der Knoblauchvorrat eines anderen Hotels reicht 39 Tage, wenn täglich 1,6 kg verbraucht werden. Aufgrund einer Änderung der Speisekarte nach 12 Tagen muss der Tagesverbrauch um 0,8 kg erhöht werden. Wie lange reicht der Vorrat insgesamt?
So geht’s:
Überlege dir zuerst, wie groß die zugeordnete Größe (hier Tage) ist.
Die 12 Tage, die bereits um sind, brauchst du erstmal nicht zu berücksichtigen. Rechne also mit 39-12=27 Tagen weiter. Das machst du wie gewohnt:
Wie lange reicht der restliche Vorrat bei 2,4 kg Tagesverbrauch?
| Knoblauchverbrauch | Anzahl der Tage |
|---|---|
| 1,6 kg | 27 |
| 0,4 kg | 108 |
| 2,4 kg | 18 |
Wie lange reicht der Vorrat insgesamt?
Addiere die bereits vergangenen Tage: 18+12=30
Der Vorrat reicht also insgesamt 30 Tage.
Ein anderes Beispiel
Der Weinkeller des Hotels muss wieder aufgefüllt werden. Anna berechnet die Kosten für den Weinlieferanten. Es fehlen 73 Flaschen Rotwein.
Sechs Flaschen Rotwein kosten 28,80 €. Ab 10 Kisten (à 6 Flaschen) kostet jede weitere Kiste nur noch 27,90 €. Für Einzelflaschen gilt aber weiterhin der normale Preis.
- Schritt: Eine Tabelle erstellen:

- Schritt: Zwischengröße finden:
Da du auch den Preis einer Einzelflasche wissen musst, bietet sich die 1 als Zwischenschritt an. (siehe Tabelle)
3. Schritt: Berechnen der fehlenden Größen:
Achtung!: Da die Zuordnung nur bis zum Rabatt (d.h. bis 60 Flaschen) proportional ist, sind zur Berechnung mehrere Einzelschritte notwendig:
- Für eine Flasche und für 60 Flaschen berechnest du den Preis mit dem Dreisatz.

- Ab 10 Kisten (60 Flaschen) gibt es für jede weitere Kiste Rabatt:
66 Flaschen kosten dann:
288 €+27,90 €=315,90 €
72 Flaschen kosten entsprechend:
288 €+2⋅27,90 €=343,80 € Für die Einzelflasche wird der Preis aus dem Zwischenschritt des Dreisatz addiert: 343,80 €+4,80 €=348,60 €
Die ausgefüllte Tabelle sieht am Ende so aus:

Die Kosten für 73 Flaschen Rotwein betragen 348,60 €.
Oft sind Dreisatzaufgaben nur in bestimmten Bereichen proportional (antiproportional). Dann musst du beim Berechnen besonders achtsam sein.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen