Funktionen

Ja, mit diesem f und x-Werten und Linien im Koordinatensystem? Klingt völlig abstrakt, kommt in der Realität aber ziemlich häufig vor.

Bisher hast du meist eine Funktionsklasse für sich gelernt: lineare Funktionen, quadratische Funktionen, Exponentialfunktionen. Aber bei welcher Anwendung nimmst du welche Funktion?

In dieser Lerneinheit geht es um etwas kompliziertere Aufgaben, für die du all dein Wissen über Funktionen zusammenbringst.

Lineare Funktion: Abbrennen einer Kerze

Titus beobachtet das Abbrennen einer 10 cm langen Kerze
und stellt fest:

• Die Kerze brennt gleichmäßig ab.
• In 10 Minuten wird die Kerze um 2 cm kürzer.

Wie lange dauert es, bis die Kerze abgebrannt ist?

Er stellt diesen Zusammenhang auf:
Brenndauer x $$rarr$$ Kerzenhöhe y.

Weil die Kerze gleichmäßig abbrennt, liegt eine lineare Funktion vor. Änderungen (Anstieg oder Abnahme) passieren bei linearen Funktionen immer gleichmäßig.

Die allgemein Funktionsgleichung linearer Funktionen lautet:
y = f(x) = mx + b mit m als Steigung und b als y-Achsenabschnitt.

Titus überlegt sich, dass zur Zeit t = 0 die Kerzenhöhe ja 10 cm beträgt. Damit hat er als Startpunkt P(0|10). Das ist gleichzeitig der Schnittpunkt mit der y-Achse und es folgt b = 10.

Als Steigung berechnet Titus: $$frac{y_2-y_1}{x_2-x_1} = -frac{2}{10}= -0,2$$.
Also lautet die Funktionsgleichung: y = f(x) = -0,2x + 10.

Der Graph:

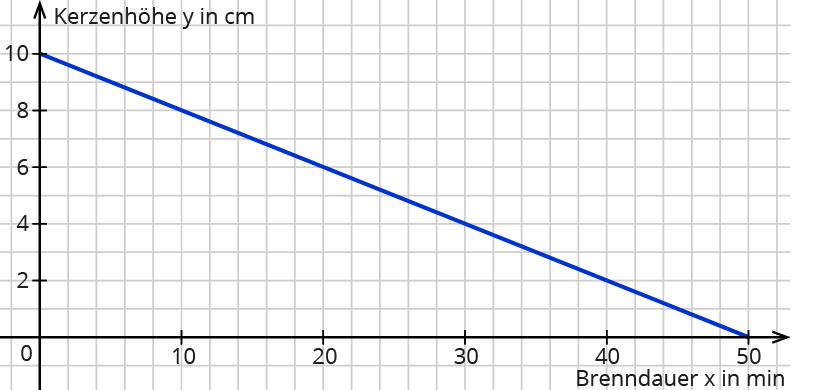
Aus diesem Graphen liest Titus ab, dass die Kerze nach 50 min abgebrannt ist. Dieses Ergebnis ist realistisch.

Bild: iStockphoto.com (kycstudio)

Die Strategie dahinter

Die meisten Anwendungsaufgaben kannst du gut mit dieser Strategie lösen:

Lösungsstrategie

1. Schritt: Aufgabe erfassen
Analysiere den Aufgabentext.
Formuliere mögliche Fragen wie z.B. „worum geht es bei dem Problem?“.
Fertige eine Skizze an.

2. Schritt: Mathematisieren
Lege fest, was die Variablen sind (meist sind es x und y).
Stelle Gleichungen ohne Einheiten auf.

3. Schritt: Lösen
Die eigentliche Lösung hängt von der Fragestellung ab:
- Lösen einer Gleichung
- Ablesen von Punkten aus einer grafischen Darstellung

4. Schritt: Ergebnis überprüfen
Ist das Ergebnis realistisch, so formuliere einen Antwortsatz mit der Lösung.
Ist das Ergebnis unrealistisch, so notiere in einem Antwortsatz die Begründung dafür, dass die Aufgabe keine Lösung hat.

Quadratische Funktion: Pizzeria

Eine Pizzeria stellt Pizzen mehrerer Größen mit den angegebenen Durchmessern her.

Die Daten können durch eine quadratische Funktion der Gestalt $$y(x) = 0,625x^2 + 5x + 1$$ modelliert werden.
a) Zeige, dass die Daten durch die Funktion $$y(x)$$ tatsächlich erfasst werden.
b) Ergibt das Modell einen vernüftigen Preis für eine Pizza mit dem Durchmesser $$28 cm$$?
c) Die Pizzeria plant eine Jumbo-Pizza mit dem Durchmesser
48 cm. Ergibt das Modell einen akzeptablen Preis für diesen Durchmesser?

Anwenden der Lösungsstrategie

1. Schritt: Aufgabe erfassen
Gegeben ist die Modellfunktion. Es soll geprüft werden, welche der angegebenen Pizzagrößen durch die Funktion beschrieben werden.
Skizze der Modellfunktion:

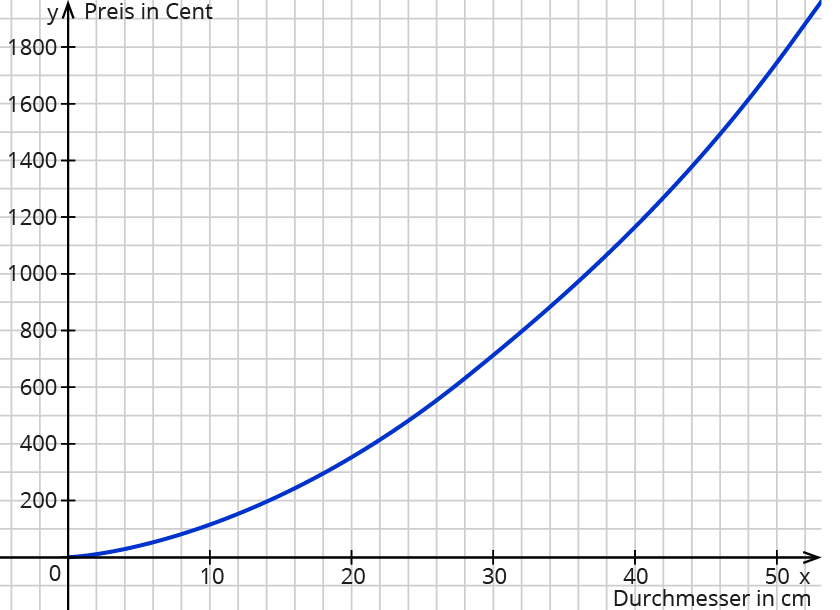
2. Schritt: Matematisieren
Dieser Schritt entfällt, da eine Modellfunktion gegeben ist.

3. Schritt: Lösen
a) Einsetzen der $$x-$$ Werte in die Modellfunktion ergibt:

1. $$y(16) = 0,625*(16)^2 + 5*16 + 1 = 241$$
   
2. $$y(20) = 0,625*(20)^2 + 5*20 + 1 = 351$$
   
3. $$y(24) = 0,625*(24)^2 + 5*24 + 1 = 481$$
   

b) Einsetzen von $$x = 28$$ in die Modellfunktion ergibt:
$$y(28) = 0,625*(28)^2 + 5*28 + 1 = 631$$

c) Einsetzen von $$x = 48$$ in die Modellfunktion ergibt:
$$y(48) = 0,625*(48)^2 + 5*48 + 1 = 1681$$

Lösungsskizze:

4. Schritt: Ergebnis überprüfen
a) Es ist gesichert, dass die gegebenen Daten durch die Modellfunktion erfasst werden.
b) Ein Preis von $$6,31 €$$ für eine Pizza dieser Größe ist bei geeigneter Belegung gerade noch akzeptabel.
c) Ein Preis von $$16,81 €$$ für eine Pizza dieser Größe ist nicht mehr akzeptabel.

Bild: Shutterstock.com/Lazhko, Svetlana

Exponentialfunktion: Radioaktiver Zerfall

Bei der Reaktorkatastrophe von Fukushima, die am 11.3.2011 begann, wurden große Mengen an radioaktivem Cäsium-137 (Cs-137) freigesetzt.
Cs-137 hat eine Halbwertszeit von 30,2 Jahren (a).
a) Bestimme das Zerfallsgesetz für eine Menge von 100 g Cs-137.
b) Berechne die Zeitdauer, bis 90 % der Anfangsmenge zerfallen sind.

Anwenden der Lösungsstrategie

1. Schritt: Aufgabe erfassen
Atomkerne radioaktiver Substanzen, wie z.B. Cs-137, zerfallen und stetzen dabei Energie und Strahlung frei. Dieser Vorgang heißt „Radioaktiver Zerfall“. Er verläuft so, dass nach einer für die radioaktive Substanz charakteristischen Zeit die Hälfte einer Anfangsmenge $$N(0)$$zerfallen ist. Diese Zeit heißt Halbwertszeit $$T_H$$.

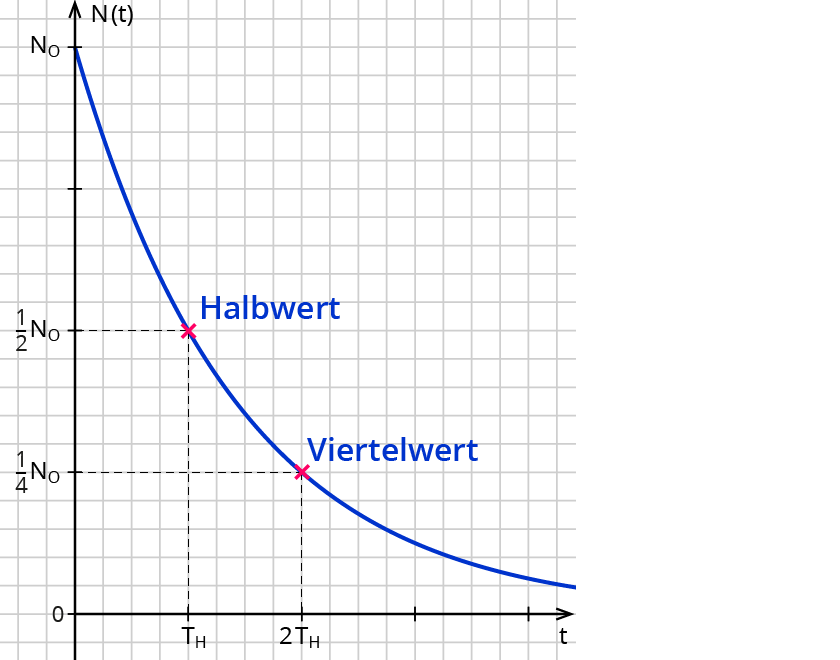
2. Schritt: Mathematisieren
Der ratioaktive Zerfall erfolgt bei einer Modellierung nach einer Exponentialfunktion: $$N(t) = N(0) * e^(-lambda*t)$$ mit $$lambda$$ als substanzspezifische Zerfallskonstante.

3. Schritt: Lösen
a) Ohne Einheiten folgt mit: N(0) = 100 der Ansatz:
$$50 = 100 * e^(-lambda*30,2)$$
Nach Division durch 100 und beidseitige ln-Bildung folgt
$$ln 0,5 =ln (e^(-lambda*30,2))$$ und weiter $$ln 0,5 = -lambda* 30,2$$.
Beachte $$ln e = 1$$
Die Auflösung nach $$lambda$$ ergibt $$lambda approx 0,023$$ und damit lautet das Zerfallsgesetz: $$N(t) = 100 * e ^(-0,023*t)$$.
b) Wenn $$90%$$ der Ausgangsmenge zerfallen sind, bleiben $$10%$$ davon übrig. Damit folgt mit dem Zerfallsgesetz:
$$10 = 100 * e^(-0,023*t)$$
Diese Gleichung wird analog zu (a) aufgelöst und ergibt $$t approx 100 a$$.

4. Schritt: Ergebnis überprüfen

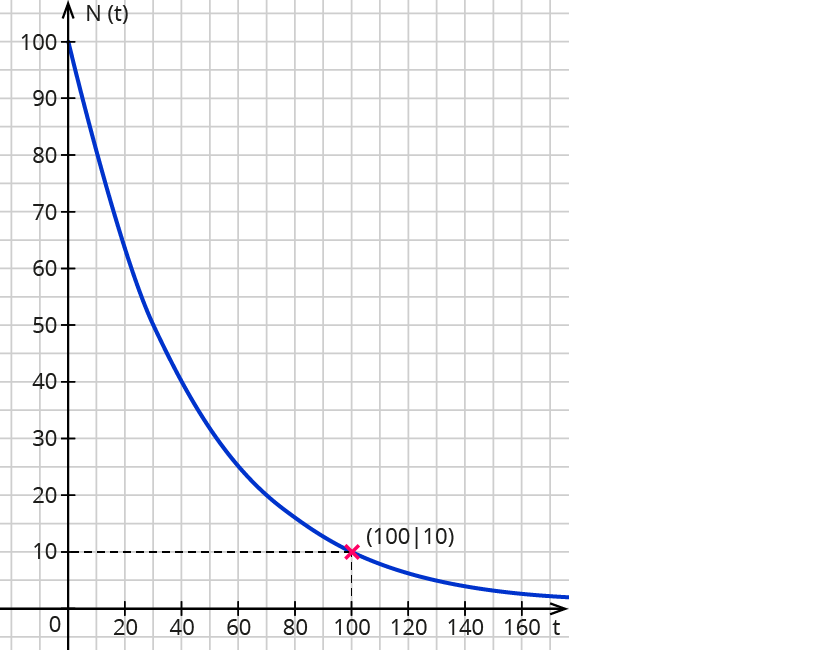
Die graphische Darstellung zeigt, dass das Zerfallsgesetz mit den gegebenen Daten eine richtige Zerfallszeit von ca. 100 Jahren ergibt.

Bild: fotolia.com (eyetronic)

Potenzfunktion: Maximales Schachtelvolumen

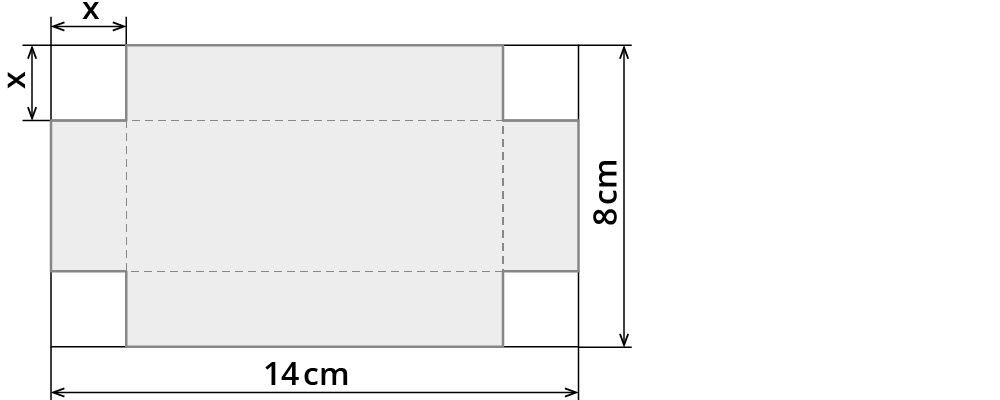
Ein Designer entfernt von einem rechteckigen Stück Blech vier gleich große Quadrate an den Ecken. Der Rest wird zu einer oben offenen Schachtel gefaltet.
a) Bestimme die Potenzfunktion $$V(x) = a * x^3 + b * x^2 + c * x + d$$, die das Volumen der Schachtel zu berechnen gestattet.
b) Finde auf Grundlage der gegebenen Werte das maximale Volumen der Schachtel.

Anwenden der Lösungsstrategie

1. Schritt: Aufgabe erfassen
Die geometrische Form der Schachtel ist ein Quader.
Das Volumen eines Quaders errechnet sich aus V = Länge x Breite x Höhe.

2. Schritt: Mathematisieren
Mit $$x$$ als Seitenlänge der fehlenden Quadrate ergibt sich das Volumen zu:
$$V(x) = x * (8 - 2x)(14 - 2x)$$

3. Lösen
a) Wird $$V(x) = x * (8 - 2x)(14 - 2x)$$ ausmultipliziert, so folgt
$$V(x) = 4x^3- 44x^2+ 112x$$
Damit haben die Koeffizienten der gesuchten Potenzfunktion die Werte:
$$a = 4, b = -44, c = 112, d = 0$$.
b) Zur näherungsweisen Bestimmung des maximalen Volumens wird der Graph der Funktion $$V = V(x)$$ erstellt.

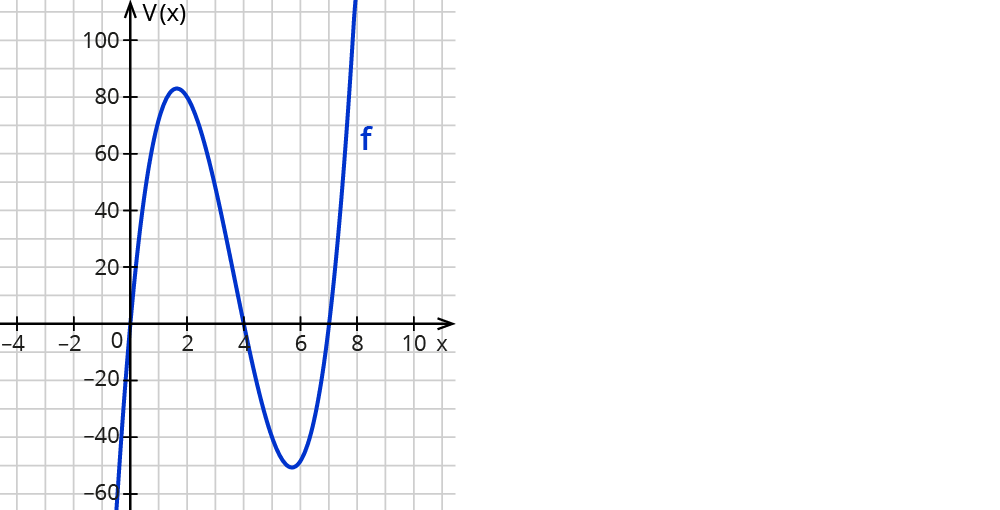
Aus dem Graphen folgt für das maximale Volumen näherungsweise $$V approx 83 cm^3 $$ bei einem Wert für $$x approx 1,64cm$$.

4. Schritt: Ergebnis überprüfen
Der Wertebereich von $$x$$ liegt im Intervall $$0 lt x lt 4$$. Damit erweisen sich die ermittelten Werte für das Volumen $$V$$ und die Seitenlänge $$x$$ als realistisch.