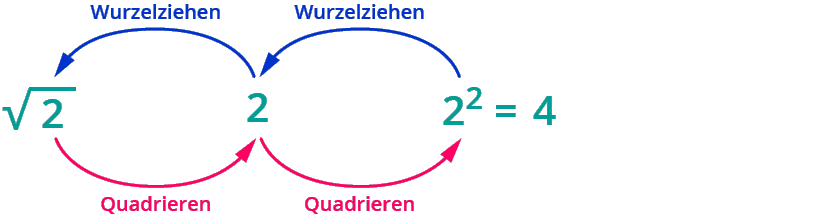
Potenzgesetze / Wurzelgesetze
Rechenregeln für Potenzen
Erinnerst du dich noch an die Potenzgesetze?
1. Potenzgesetz
am⋅an=am+n
aman=am-n mit a≠0
2. Potenzgesetz
an⋅bn=(a⋅b)n
anbn=(ab)n mit b≠0
3. Potenzgesetz: Potenzen potenzieren
(an)m=an⋅m
Bisher hast du für m und n ganze Zahlen eingesetzt.
Die Potenzgesetze gelten aber auch für Brüche im Exponenten! Mathematisch genau: wenn die Exponenten rationale Zahlen sind.
Die Gesetze gelten, wenn m,n∈ℚ.
Die Potenzgesetze gelten nicht nur für Exponenten aus den ganzen Zahlen ℤ, sondern für Exponenten aus den rationalen Zahlen ℚ.
Ganze Zahlen ℤ sind ℤ={…-3;-2;-1;0;1;2;3;…}
Die rationalen Zahlen ℚ sind positive und negative Brüche:
ℚ={pq∣p,q∈ℤ;q≠0}
Beispiele
1. Potenzgesetz
Vereinfache. Rechne so viel wie möglich ohne Taschenrechner.
213⋅223=213+23=21=2
144-32⋅1442=144-32+42=14412=√144=12
x114x34=x114-34=x84=x2
2. Potenzgesetz
412⋅1612=(4⋅16)12=6412=8
3234234=(322)34=1634=8
3. Potenzgesetz: Potenzen potenzieren
(312)4=312⋅4=32=9
(4916)-3=4916⋅(-3)=49-36=49-12=14912=1√49=17
Und wie sieht’s mit Wurzeln aus? Kannst du die Gesetze auf n-te Wurzeln übertragen?
Für das 1. Potenzgesetz gibt es keine Entsprechung bei den Wurzeln, aber für die anderen zwei!
Zur Erinnerung:
1. Potenzgesetz:
am⋅an=am+n
aman=am-n mit a≠02. Potenzgesetz
an⋅bn=(a⋅b)n
anbn=(ab)n mit b≠03. Potenzgesetz: Potenzen potenzieren
(an)m=an⋅m
Die n-te Wurzel aus einem Produkt
Versuche, mithilfe der Potenzgesetze Wurzelterme umzuformen.
Beispiel:
√4⋅√9?=√4⋅9
Los geht’s mit √4⋅√9
Umwandeln in Potenzen:
√4⋅√9=412⋅912
Anwenden des 1. Potenzgesetzes:
412⋅912=(4⋅9)12
Umwandeln in eine Wurzel:
(4⋅9)12=√4⋅9
In Kurzform:
√4⋅√9=412⋅912=(4⋅9)12=√4⋅9
Das wolltest du zeigen.
Diese Rechnung kannst du für alle möglichen Zahlen, also auch allgemein für Radikanden a und b und Exponenten n durchführen. (Die Radikanden dürfen natürlich nicht negativ sein.)
Willst du n-te Wurzeln multiplizieren, multipliziere die Radikanden. Die Wurzel bleibt gleich.
n√a⋅n√b=n√a⋅b für jede natürliche Zahl n,
a, b≥0
Zur Erinnerung:
2. Potenzgesetz
an⋅bn=(a⋅b)n
anbn=(ab)n mit b≠0n√x=x1n
Zur Kontrolle:
√4⋅√9=2⋅3=6
√4⋅9=√36=6

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Und die Division?
Wie mit Produkten kannst du dir auch die Regel zur Wurzel aus Quotienten überlegen.
Beispiel 1:
4√164√81=16148114=(1681)14=4√1681
Beispiel 2:
Andersum ist es manchmal praktisch zum Rechnen: 4√1681=4√164√81=23
Willst du n-te Wurzeln dividieren, dividiere die Radikanden. Die Wurzel bleibt gleich.
n√an√b=n√ab für jede natürliche Zahl n,
a≥0 und b>0
Zur Erinnerung:
2. Potenzgesetz
an⋅bn=(a⋅b)n
anbn=(ab)n mit b≠0n√x=x1n
Die Wurzel in der Wurzel
Untersuche die letzte Rechenregel: Was passiert, wenn du die Wurzel aus einer Wurzel ziehst?
Beispiel:
2√5√59049=(5904915)12=59049110=10√59049
Also: 2√5√59049=2⋅5√59049
Und allgemein:
Willst du eine Wurzel aus einer Wurzel ziehen, multipliziere die Wurzelexponenten.
m√n√a=m⋅n√a für natürliche Zahlen n und m
a≥0
Zur Erinnerung:
Potenzen potenzieren:
(an)m=an⋅mn√x=x1n
Beispiele
4√162⋅4√8=4√162⋅8=4√1296=6
6√53√5=6√5⋅13√5=516⋅5-13=516-13=5-16=16√5
12√64=3⋅4√64=4√3√64=4√4=2⋅2√4=√√4=√2
Nicht durcheinanderkommen: √ ist die 2. Wurzel, nicht etwa die 1. :-)
Die Wurzelgesetze
- n√a⋅n√b=n√a⋅b
n∈ℕ, a, b≥0 - n√an√b=n√ab
n∈ℕ, a≥0 und b>0 - m√n√a=m⋅n√a
m,n∈ℕ, a≥0

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen