Prisma – Wie berechne ich das Volumen eines Prismas?
Was ist das Volumen von Prismen?
Da Prismen Körper sind, können sie gefüllt werden.
Füllst du ein Prisma mit Wasser und misst dies in einem Messbecher, erhältst du das Volumen des Prismas. Das Volumen gibt dir an, wie viel Flüssigkeit in ein Prisma passt.
Man kann Prismen ebenso mit Einheitswürfeln füllen. Das Volumen des Prismas gibt dann an, wie viele Einheitswürfel in das Prisma passen.
Bei Prismen mit „spitzen“ Ecken geht das Auslegen mit den Einheitswürfeln nicht mehr so gut.

Aber du kannst eine Formel nehmen, die für alle geraden Körper passt: Grundfläche $$*$$ Höhe
So berechnest du das Volumen eines Prismas:
- Berechne die Grundfläche.
- Berechne das Volumen. Volumen $$=$$ Grundfläche $$*$$ Körperhöhe. Kurzschreibweise: $$V = G * h_k$$


Ein Einheitswürfel hat die Kantenlänge $$a = 1$$ $$cm$$ und somit das Volumen $$V = 1$$ $$cm^3$$.
Das Volumen wird in $$cm^3$$ (sprich: Kubikzentimeter) angegeben.
Los geht’s: das Dreiecksprisma
Gegeben ist ein Dreiecksprisma mit den Kantenlängen
$$a = 4$$ $$cm$$,
$$b = h_a = 3$$ $$cm$$,
$$h_k = 2$$ $$cm$$.

Um das Volumen zu berechnen, gehe so vor:
1. Berechne die Grundfläche.
Die Grundfläche ist ein rechtwinkliges Dreieck.
$$G = 1/2 g * h$$ (beliebiges Dreieck)
$$G = 1/2 a * b$$ (rechtwinkliges Dreieck)
$$G = 1/2 4$$ $$cm * 3$$ $$cm$$
$$G = 1/2 12$$ $$cm^2$$
$$G = 6$$ $$cm^2$$
Für die Grundseite $$g$$ nimmst du die Seite $$a$$, für $$h$$ die Seite $$b$$. Da es ein rechtwinkliges Dreieck ist, ist die Seite $$b$$ auch gleichzeitig die Dreieckshöhe $$h_a$$ zur Seite $$a$$ (im rechten Winkel dazu).
2. Berechne das Volumen.
Volumen $$=$$ Grundfläche $$*$$ Körperhöhe
$$V = G * h_k$$
$$V = 6$$ $$cm^2 * 2$$ $$cm$$
$$V = 12$$ $$cm^3$$
$$h_a$$ bezeichnet die Höhe der Dreiecksseite $$a$$.
Flächeninhalt eines Dreiecks: $$G = 1/2 g * h$$

- $$g$$ Grundseite
- $$h$$ Höhe des Dreiecks
Tipp:
Die Höhe der Grundfläche ist nicht die Höhe des Körpers $$h_k$$.
Volumen beliebiger Prismen berechnen
Prismen können verschiedene Grundflächen haben.
Je nachdem, um welches Prisma es sich handelt, rechnest du mit anderen Formeln die Grundfläche $$G$$.
| Grundfläche des Prismas | Benutze folgende Formeln: |
|---|---|
| Dreieck | |
| Parallelogramm | |
| Trapez |
Dann rechnest du immer:
Volumen $$=$$ Grundfläche $$*$$ Körperhöhe
| Grundfläche des Prismas | Benutze folgende Formeln: |
|---|---|
| Quadrat | |
| Rechteck |
$$V = G * h_k$$
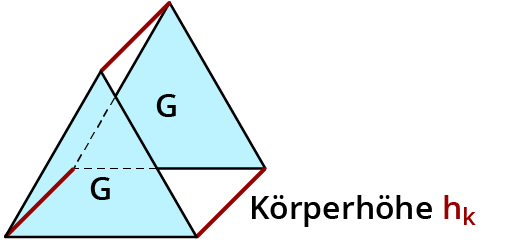
Die Körperhöhe $$h_k$$ ist die Strecke, welche die beiden Grundflächen miteinander verbindet:

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen