Satz des Pythagroas: Streckenlängen berechnen
Immer diese Dreiecke
Du lernst in diesem Kapitel neue Begriffe und Rechnungen für das rechtwinklige Dreieck kennen. Alles, was du jetzt lernst, gilt ausschließlich in rechtwinkligen Dreiecken.
Neue Begriffe
Im rechtwinkligen Dreieck heißen die Seiten Katheten und Hypotenuse. Die längste Seite heißt Hypotenuse. Die beiden kürzeren Seiten heißen Katheten. Die Hypotenuse liegt immer dem rechten Winkel gegenüber.
Diese Namen der Seiten klingen griechisch, sind sie auch. Das liegt daran, dass die Rechnungen im rechtwinkligen Dreieck von einem Griechen herausgefunden worden sind. Er hat die Seiten so getauft. Du ahnst es: Der Grieche hieß Pythagoras.


Bild: The Art Archive (Alfredo Dagli Orti)
Pythagoras (ca. 570-510 v. Chr.)
Der Satz von Pythagoras
Pythagoras ist der Grieche, der die Berechnung im rechtwinkligen Dreieck herausgefunden hat.
Der Pythagoras in Wort und Bild
In Worten
Pythagoras fand heraus, dass das Hypotenusenquadrat flächeninhaltsgleich zu den beiden Kathetenquadraten ist.
Im Bild

Ohne das Dreieck sieht das so aus:


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Der Pythagoras mit Buchstaben
Beim Satz des Pythagoras werden Flächen miteinander gleichgesetzt.

Um den Flächeninhalt der einzelnen Quadrate auszudrücken, wendest du die Formel zum Flächeninhaltsberechnen eines Quadrates an.
Für das Hypotenusenquadrat:
A□=c⋅c=c2
Für die beiden Kathetenquadrate:
A□=a⋅a=a2
A□=b⋅b=b2
Der Satz des Pythagoras heißt allgemeingültig: c2=a2+b2
Gleichbedeutend ist die Formel:
a2+b2=c2
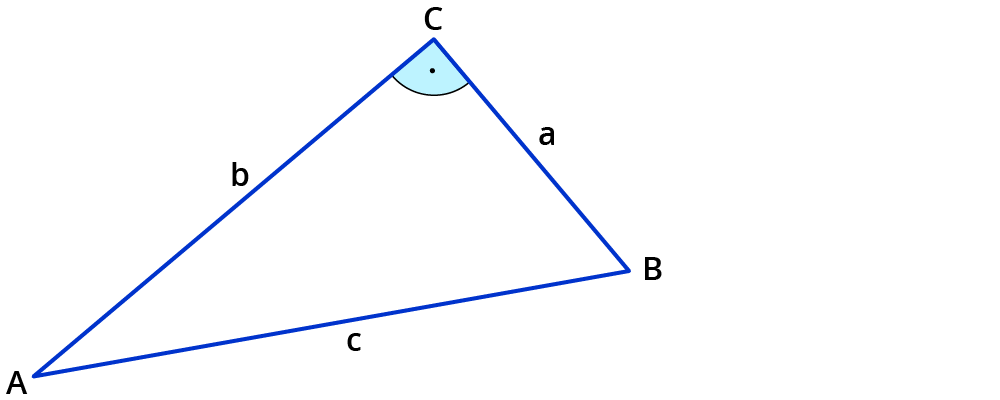
Im Dreieck werden die Seiten auch mit den Kleinbuchstaben a, b und c bezeichnet.
Die Beschriftung erfolgt in der Regel gegen den Uhrzeigersinn. Die längste Seite wird oft mit c betitelt - die Hypotenuse ist jetzt c.

Diese Formel findest du nahezu überall. Sie gilt, wenn a und b die Katheten sind und c die Hypotenuse. Natürlich kannst du den Dreiecksseiten andere Namen geben. Dann sieht auch der Satz des Pythagoras anders aus.

Es gilt ♡2+y2=x2.
Umstellen der Formel
Es gibt Situationen, in denen du nicht die längste Seite ausrechnen möchtest, sondern eine Kathete. Dann stellst du die Formel um.
a2+b2=c2 ∣-a2
b2=c2-a2
oder
a2+b2=c2 ∣-b2
a2=c2-b2
Immer wenn du eine Kathete berechnen möchtest, ist der Satz des Pythagoras eine Minus-Aufgabe. Von dem Hypotenusenquadrat wird ein Kathetenquadrat abgezogen.
Anders herum geht die -Aufgabe nicht, denn das Hypotenusenquadrat ist größer als der Flächeninhalt von dem Kathetenquadrat.
Ja und?
Solltest du jetzt denken, dass das nichts Atemberaubendes ist, liegst du falsch. :-) Mit dem Satz des Pythagoras kannst du viele Herausforderungen lösen.
Zum Beispiel:
Wie hoch reicht eine 4 m lange Leiter hinauf, wenn du sie 1,5 m entfernt von der Hauswand aufstellst?

In dieser Aufgabe liegt ein rechtwinkliges Dreieck, also kannst du den Satz des Pythagoras anwenden, um die fehlende Seite im Dreieck zu berechnen.
(Solche Berechnungen können Leben retten, wenn es zum Beispiel in einem Haus brennt und die Feuerwehr mit dem richtigen Leiterwagen zur Rettung eilt.)

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Jetzt wird gerechnet
Als erstes lernst du, die Hypotenuse eines rechtwinkligen Dreiecks zu berechnen.
Gegeben ist:
a=3 cm und b=4 cm - die Katheten
Gesucht ist :
c - die Hypotenuse
Notiere den Satz des Pythagoras, den du verwendest.
c2=a2+b2
Setze die Zahlen ein.
c2=32+42
Rechne so weit wie möglich aus.
c2=9+16
c2=25
Da du nicht das Hypotenusenquadrat berechnen möchtest, sondern die Hypotenuse, die Länge dieser Seite, musst du jetzt auf beiden Seiten der Gleichung die Wurzel ziehen.
c2=25 ∣√
c=5
c ist 5 cm lang.
Rechnung auf einen Blick:
c2=a2+b2
c2=32+42
c2=9+16
c2=25 ∣√
c=5
Für den Pythagoras solltest du fit mit Wurzeln und Potenzen (Hochzahlen) sein.
Wenn die Wurzel aus dem Hypotenusenquadrat gezogen wird, kann es sein, dass du eine unendliche Dezimalzahl als Ergebnis bekommst. Runde dann dein Ergebnis. In der Aufgabenstellung steht, auf wie viele Nachkommastellen. Oder dein Lehrer sagt es dir.
Weiter gerechnet
Du lernst jetzt, wie du eine der Katheten im rechtwinkligen Dreieck berechnen kannst.
Gegeben sind die Längen c=5 cm (Hypotenuse) und a=3 cm. Gesucht ist die Kathete b.
Notiere die Formel, die du verwendest.
b2=c2-a2
Setze die Zahlen ein.
b2=52-32
Rechne so weit wie möglich aus:
b2=25-9
b2=16
Jetzt ziehst du die Wurzel auf beiden Seiten der Gleichung. Bisher hast du nur den Flächeninhalt von der Kathete b berechnet. Du willst aber die Länge der Kathete herausbekommen.
b2=16 ∣√
b=4
b ist 4 cm lang.
Auch bei dieser Rechnung bekommst du nach dem Wurzelziehen oft eine unendliche Dezimalzahl heraus. Runden nicht vergessen. :-)
Die Rechnung mal anders
Du kannst die Rechnung für die Hypotenuse auch anders notieren. Sie berechnet dasselbe.
Gegeben ist:
a=3 cm und b=4 cm - die Katheten
Gesucht ist:
c - die Hypotenuse
Der Unterschied ist, dass du gleich nach c (die Länge, nicht das Quadrat) umstellst.
Dann musst du die Wurzel aber sofort über den anderen Teil der Gleichung setzen.
c2=a2+b2 ∣√
c=√a2+b2
c=√32+42
c=√9+16
c=√25
c=5
Auch die Kathetenberechnung kannst du genauso gleich unter einer Wurzel notieren.
Du nimmst den Rechenweg, der dir besser gefällt.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Ist ein Dreieck rechtwinklig?
Wenn du 3 Längen eines Dreiecks gegeben hast, kannst du mithilfe des Satzes von Pythagoras prüfen, ob das Dreieck rechtwinklig ist.
Das Dreieck ist rechtwinklig, wenn die Gleichung Hypotenuse² = erste Kathete² + zweite Kathete² gilt. Wenn die Gleichung nicht gilt (auf beiden Seiten der Gleichung stehen nach der Ausrechnung verschiedene Zahlen), ist das Dreieck nicht rechtwinklig.
Beispiel:
Gegeben ist ein Dreieck mit a=4 cm, b=5 cm und c=6 cm. Ist dieses Dreieck rechtwinklig?
Es gilt:
c2=36
und
a2+b2=42+52=16+25=41.
Also gilt c2≠a2+b2. Deshalb ist das Dreieck nicht rechtwinklig.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen